Композиция функций
Мы научились комбинировать функции наиболее общего типа a -> b. В этой главе мы посмотрим на специальные функции и способы их комбинирования. Специальными функциями мы будем называть такие функции, результат которых имеет некоторую известную нам структуру. Среди них функции, которые могут вычислить значение или упасть, или функции, которые возвращают сразу несколько вариантов значений. Для составления таких функций из простейших в Haskell предусмотрено несколько классов типов. Это функторы и монады. Их мы и рассмотрим в этой главе.
Центральной функцией этой главы будет функция композиции. Вспомним её определение для функций общего типа:
(.) :: (b -> c) -> (a -> b) -> (a -> c) f . g = \x -> f (g x)
Композиция двух функций f и g это такая функция, в которой мы сначала применяем g, а затем f. Для того чтобы тип функции стал более наглядным, мы определим эту функцию немного по-другому. Мы поменяем аргументы местами.
(>>) :: (a -> b) -> (b -> c) -> (a -> c) f >> g = \x -> g (f x)
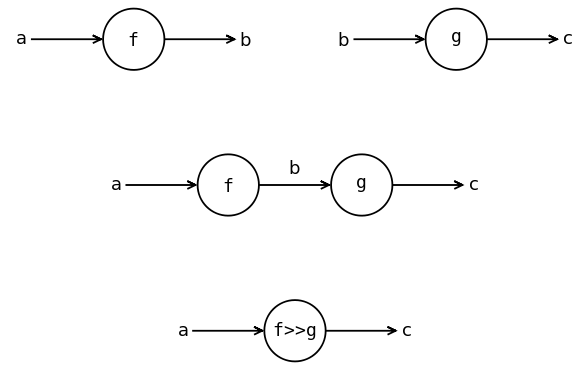
Мы будем изображать функции кружками, а значения – стрелками. Значения словно текут от узла к узлу по стрелкам. Поскольку тип стрелки выходящей из f совпадает с типом стрелки входящей в g мы можем соединить их и получить составную функцию (f >> g).

Композиция функций
С помощью операции композиции можно обобщить понятие функции. Для этого существует класс Category:
class Category cat where
id :: cat a a
(>>) :: cat a b -> cat b c -> cat a c
Функция cat это тип с двумя параметрами, в котором выделено специальное значение id, которое оставляет аргумент без изменений. Также мы можем составлять из простых функций сложные с помощью композиции, если функции совпадают по типу. Здесь мы для наглядности также заменили метод (.) на (>>), но суть остаётся прежней. Для любого экземпляра класса должны выполняться свойства:
f >> id == f id >> f == f f >> (g >> h) == (f >> g) >> h
Первые два свойства говорят о том, что id является нейтральным элементом для (>>) слева и справа. Третье свойство говорит о том, что нам не важно в каком порядке проводить композицию. Можно проверить, что эти правила выполнены для функций.
Все специальные функции, которые мы рассмотрим в этой главе будут иметь один и тот же тип:
a -> m b
Смотрите вместо произвольного типа b функция возвращает m b. Единственное, что будет меняться от раздела к разделу это тип m. Добавив этот тип к результату, мы сузили область значений функции. Простым примером таких функций могут быть функции, которые возвращают списки:
a -> [b]
Если раньше наши функции могли возвращать произвольное значение b, то теперь мы знаем, что все результирующие значения таких функций будут списками.
При этом для каждого такого m мы попытаемся построить свой замкнутый мир специальных функций a -> m b. Он будет жить внутри вселенной всех произвольных функций типа a -> b. В этом нам поможет специальный класс типов, который называется категорией Клейсли (эта конструкция носит имя математика Хенрика Клейсли).
class Kleisli m where
idK :: a -> m a
(*>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
Этот класс является классом Category в мире наших специальных функций. Если мы сотрём все буквы m, то мы получим обычные типы для тождества и композиции. В этом мире должны выполняться те же правила:
f *> idK == f idK *> f == f f *> (g *> h) == (f *> g) *> h
С помощью класса Kleisli мы можем составлять из одних специальных функций другие. Но как мы сможем комбинировать специальные функции с обычными?
Поскольку слева у нашей специальной функции обычный общий тип, то с этой стороны мы можем воспользоваться обычной функцией композиции >>. Но как быть при композиции справа? Нам нужна функция типа:
(a -> m b) -> (b -> c) -> (a -> m c)
Оказывается мы можем составить её из методов класса Kleisli. Мы назовём эту функцию композиции (+>).
(+>) :: Kleisli m => (a -> m b) -> (b -> c) -> (a -> m c) f +> g = f *> (g >> idK)
С помощью метода idK мы можем погрузить в мир специальных функций любую обычную функцию.
У нас появилось много композиций целых три:
аргументы | результат обычная >> обычная == обычная специальная +> обычная == специальная специальная *> специальная == специальная
При этом важно понимать, что по смыслу это три одинаковые функции. Они обозначают операцию последовательного применения функций. Разные значки отражают разные типы функций аргументов. Определим модуль Kleisli.hs
module Kleisli where
import Prelude hiding (id, (>>))
class Category cat where
id :: cat a a
(>>) :: cat a b -> cat b c -> cat a c
class Kleisli m where
idK :: a -> m a
(*>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
(+>) :: Kleisli m => (a -> m b) -> (b -> c) -> (a -> m c)
f +> g = f *> (g >> idK)
-- Экземпляр для функций
instance Category (->) where
id = \x -> x
f >> g = \x -> g (f x)
Мы не будем импортировать функцию id, а определим её в классе Category. Также в Prelude уже определена функция (>>) мы спрячем её с помощью специальной директивы hiding для того, чтобы она нам не мешалась. Далее мы будем дополнять этот модуль экземплярами класса Kleisli и примерами.
Частично определённые функции – это такие функции, которые определены не для всех значений аргументов. Примером такой функции может быть функция поиска предыдущего числа для натуральных чисел. Поскольку числа натуральные, то для нуля такого числа нет. Для описания этого поведения мы можем воспользоваться специальным типом Maybe. Посмотрим на его определение:
data Maybe a = Nothing | Just a
deriving (Show, Eq, Ord)

Частично определённая функция
Частично определённая функция имеет тип a -> Maybe b, если всё в порядке и значение было вычислено, она вернёт (Just a), а в случае ошибки будет возвращено значение Nothing. Теперь мы можем определить нашу функцию так:
pred :: Nat -> Maybe Nat pred Zero = Nothing pred (Succ a) = Just a
Для Zero предыдущий элемент не определён .
Значение функции pred завёрнуто в упаковку Maybe, и для того чтобы воспользоваться им нам придётся разворачивать его каждый раз. Как будет выглядеть функция извлечения дважды предыдущего натурального числа:
pred2 :: Nat -> Maybe Nat
pred2 x =
case pred x of
Just (Succ a) -> Just a
_ -> Nothing
Если мы захотим определить pred3, мы заменим pred в case-выражении на pred2. Не такое уж и длинное решение, но всё же мы теряем все преимущества гибких функций, все преимущества бесточечного стиля. Нам бы хотелось написать так:
pred2 :: Nat -> Maybe Nat pred2 = pred >> pred pred3 :: Nat -> Maybe Nat pred3 = pred >> pred >> pred
Но компилятор этого не допустит.
Для того чтобы понять как устроена композиция частично определённых функций изобразим её вычисление графически. Сверху изображены две частично определённых функции. Если функция f вернула значение, то оно подставляется в следующую частично определённую функцию. Если же первая функция не смогла вычислить результат и вернула Nothing, то считается что вся функция (f*>g) вернула Nothing.
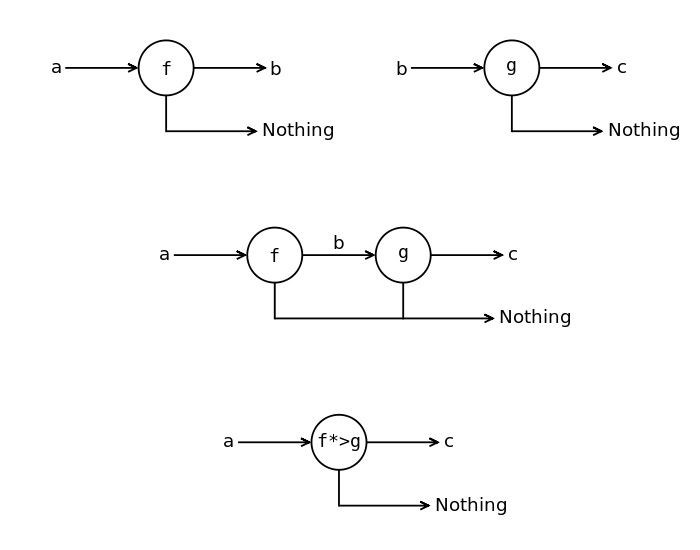
Композиция частично определённых функций
Теперь давайте закодируем это определение в Haskell. При этом мы воспользуемся нашим классом Kleisli. Аналогом функции id для частично определённых функций будет функция, которая просто заворачивает значение в конструктор Just.
instance Kleisli Maybe where
idK = Just
f *> g = \a -> case f a of
Nothing -> Nothing
Just b -> g b
Смотрите, в case-выражении мы возвращаем Nothing, если функция f вернула Nothing, а если ей удалось вычислить значение и она вернула (Just b) мы передаём это значение в следующую функцию, то есть составляем выражение (g b).
Сохраним это определение в модуле Kleisli, а также определение для функции pred и загрузим модуль в интерпретатор. Перед этим нам придётся добавить в список функций, которые мы не хотим импортировать из Prelude функцию pred, она также уже определена в Prelude. Для определения нашей функции нам потребуется модуль Nat, который мы уже определили. Скопируем файл Nat.hs в ту же директорию, в которой содержится файл Kleisli.hs и подключим этот модуль. Шапка модуля примет вид:
module Kleisli where
import Prelude hiding(id, (>>), pred)
import Nat
Добавим определение экземпляра Kleisli для Maybe в модуль Kleisli а также определение функции pred. Сохраним обновлённый модуль и загрузим в интерпретатор.
*Kleisli> :load Kleisli [1 of 2] Compiling Nat ( Nat.hs, interpreted ) [2 of 2] Compiling Kleisli ( Kleisli.hs, interpreted ) Ok, modules loaded: Kleisli, Nat. *Kleisli> let pred2 = pred *> pred *Kleisli> let pred3 = pred *> pred *> pred *Kleisli> let two = Succ (Succ Zero) *Kleisli> *Kleisli> pred two Just (Succ Zero) *Kleisli> pred3 two Nothing
Обратите внимание на то, как легко определяются производные функции. Желаемое поведение для частично определённых функций закодировано в функции (*>) теперь нам не нужно заворачивать значения и разворачивать их из типа Maybe.
Приведём пример функции, которая составлена из частично определённой функции и обычной. Определим функцию beside, которая вычисляет соседей для данного числа Пеано.
*Kleisli> let beside = pred +> \a -> (a, a + 2) *Kleisli> beside Zero Nothing *Kleisli> beside two Just (Succ Zero,Succ (Succ (Succ Zero))) *Kleisli> (pred *> beside) two Just (Zero,Succ (Succ Zero))
В выражении
pred +> \a -> (a, a + 2)
Мы сначала вычисляем предыдущее число, и если оно есть составляем пару из \a -> (a, a+2), в пару попадёт данное число и число, следующее за ним через одно. Поскольку сначала мы вычислили предыдущее число в итоговом кортеже окажется предыдущее число и следующее.
Итак с помощью функций из класса Kleisli мы можем составлять частично определённые функции в бесточечном стиле. Обратите внимание на то, что все функции кроме pred были составлены в интерпретаторе.
Отметим, что в Prelude определена специальная функция maybe, которая похожа на функцию foldr для списков, она заменяет в значении типа Maybe конструкторы на функции. Посмотрим на её определение:
maybe :: b -> (a -> b) -> Maybe a -> b maybe n f Nothing = n maybe n f (Just x) = f x
С помощью этой функции мы можем переписать определение экземпляра Kleisli так:
instance Kleisli Maybe where
idM = Just
f *> g = f >> maybe Nothing g
Многозначные функции ветрены и непостоянны. Для некоторых значений аргументов они возвращают одно значение, для иных десять, а для третьих и вовсе ничего. В Haskell такие функции имеют тип a -> [b]. Функция возвращает список ответов. На рисунке изображена схема многозначной функции.

Многозначная функция
Приведём пример. Системы Линденмайера (или L-системы) моделируют развитие живого организма. Считается, что организм состоит из последовательности букв (или клеток). В каждый момент времени одна буква заменяется на новую последовательность букв, согласно определённым правилам. Так организм живёт и развивается. Приведём пример:
| $a \rightarrow ab$ |
| $b \rightarrow a$ |
| $a$ |
| $ab$ |
| $aba$ |
| $abaab$ |
| $abaababa$ |
У нас есть два правила размножения клеток-букв в организме. На каждом этапе мы во всём слове заменяем букву $a$ на слово $ab$ и букву $b$ на $a$. Начав с одной буквы $a$, мы за несколько шагов пришли к более сложному слову.
Опишем этот процесс в Haskell. Для этого определим правила развития организма в виде многозначной функции:
next :: Char -> String next 'a' = "ab" next 'b' = "a"
Напомню, что строки в Haskell являются списками символов. Теперь нам нужно применить многозначную функцию к выходу многозначной функции. Для этого мы воспользуемся классом Kleisli.
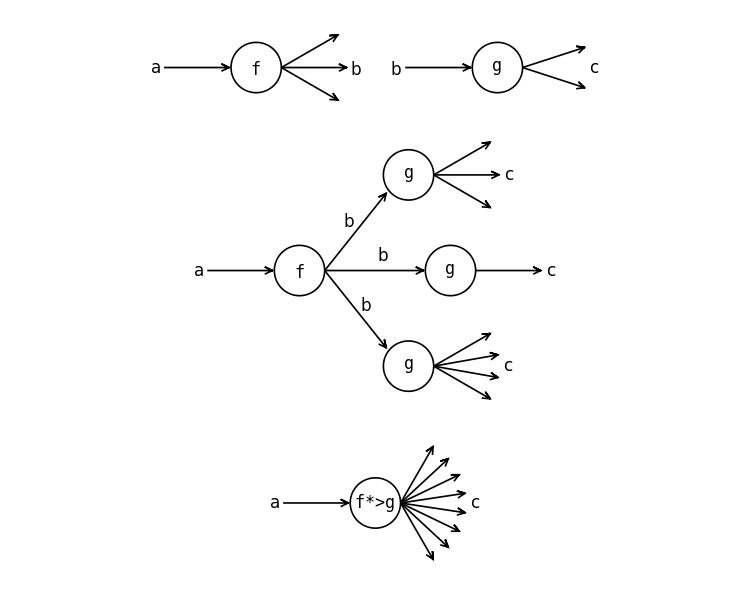
Композиция многозначных функций
Определим экземпляр класса Kleisli для списков. На рисунке изображена схема композиции в случае многозначных функций. После применения первой функции f мы применяем функцию к каждому элементу списка, который был получен из f. Так у нас получится список списков. Но нам нужен список, для этого мы после применения g объединяем все значения в один большой список. Отметим, что функции f и g в зависимости от значений могут возвращать разное число значений, поэтому на выходе у функций g разное число стрелок.
Закодируем эту схему в Haskell:
instance Kleisli [] where
idK = \a -> [a]
f *> g = f >> map g >> concat
Функция тождества принимает одно значение и погружает его в список. В композиции мы сначала применяем f, затем к каждому элементу списка результата применяем g, так у нас получается список списков. После чего мы сворачиваем его в один список с помощью функции concat.
Вспомним тип функций map и concat:
map :: (a -> b) -> [a] -> [b] concat :: [[a]] -> [a]
С помощью композиции мы можем получить n-тое поколение так:
generate :: Int -> (a -> [a]) -> (a -> [a]) generate 0 f = idK generate n f = f *> generate (n - 1) f
Или мы можем воспользоваться функцией iterate и написать это определение так:
generate :: Int -> (a -> [a]) -> (a -> [a]) generate n f = iterate (*> f) idK !! n
Функция iterate принимает функцию вычисления следующего элемента и начальное значение и строит бесконечный список итераций:
iterate :: (a -> a) -> a -> [a] iterate f a = [a, f a, f (f a), f (f (f a)), ...]
Если мы подставим наши аргументы то мы получим список:
[id, f, f*>f, f*>f*>f, f*>f*>f*>f, ...]
Проверим как работает эта функция в интерпретаторе. Для этого мы сначала дополним наш модуль Kleisli определением экземпляра для списков и функциями next и generate:
*Kleisli> :reload [2 of 2] Compiling Kleisli ( Kleisli.hs, interpreted ) Ok, modules loaded: Kleisli, Nat. *Kleisli> let gen n = generate n next 'a' *Kleisli> gen 0 "a" *Kleisli> gen 1 "ab" *Kleisli> gen 2 "aba" *Kleisli> gen 3 "abaab" *Kleisli> gen 4 "abaababa"
Правила L-системы задаются многозначной функцией. Функция generate позволяет по такой функции строить произвольное поколение развития буквенного организма.
Давайте определим в терминах композиции ещё одну полезную функцию. А именно функцию применения. Вспомним её тип:
($) :: (a -> b) -> a -> b
Эту функцию можно определить через композицию, если у нас есть в наличии постоянная функция и единичный тип. Мы будем считать, что константа это функция из единичного типа в значение. Превратив константу в функцию мы можем составить композицию:
($) :: (a -> b) -> a -> b f $ a = (const a >> f) ()
В самом конце мы подставляем специальное значение (). Это значение единичного типа (unit type) или кортежа с нулём элементов. Единичный тип имеет всего одно значение, которым мы и воспользовались в этом определении. Зачем такое запутанное определение, вместо привычного (f a)? Оказывается точно таким же способом мы можем определить применение в нашем мире специальных функций a -> m b.
Применение в этом мире происходит особенным образом. Необходимо помнить о том, что второй аргумент функции применения, значение, которое мы подставляем в функцию, также было получено из какой-то другой функции. Поэтому оно будет иметь такую же форму, что и значения справа от стрелки. В нашем случае это m b.
Посмотрим на типы специальных функций применения:
(*$) :: (a -> m b) -> m a -> m b (+$) :: (a -> b) -> m a -> m b
Функция *$ применяет специальную функцию к специальному значению, а функция +$ применяет обычную функцию к специальному значению. Определения выглядят также как и в случае обычной функции применения, мы только меняем знаки для композиции:
f $ a = (const a >> f) () f *$ a = (const a *> f) () f +$ a = (const a +> f) ()
Теперь мы можем не только нанизывать специальные функции друг на друга но и применять их к значениям. Добавим эти определения в модуль Kleisli и посмотрим как происходит применение в интерпретаторе. Одна тонкость заключается в том, что мы определяли применение в терминах класса Kleisli, поэтому правильно было написать типы новых функций так:
infixr 0 +$, *$ (*$) :: Kleisli m => (a -> m b) -> m a -> m b (+$) :: Kleisli m => (a -> b) -> m a -> m b
Также мы определили приоритет выполнения операций.
Загрузим в интерпретатор:
*Kleisli> let three = Succ (Succ (Succ Zero)) *Kleisli> pred *$ pred *$ idK three Just (Succ Zero) *Kleisli> pred *$ pred *$ idK Zero Nothing
Обратите внимание на то как мы погружаем в мир специальных функций обычное значение с помощью функции idK.
Вычислим третье поколение L-системы:
*Kleisli> next *$ next *$ next *$ idK 'a' "abaab"
Мы можем использовать и другие функции на списках:
*Kleisli> next *$ tail $ next *$ reverse $ next *$ idK 'a' "aba"
С помощью функции +$ мы можем применять к специальным значениям обычные функции одного аргумента. А что если нам захочется применить функцию двух аргументов?
Например если мы захотим сложить два частично определённых числа:
?? (+) (Just 2) (Just 2)
На месте ?? должна стоять функция типа:
?? :: (a -> b -> c) -> m a -> m b -> m c
Оказывается с помощью методов класса Kleisli мы можем определить такую функцию для любой обычной функции, а не только для функции двух аргументов. Мы будем называть такие функции словом liftN, где N – число, указывающее на арность функции. Функция (liftN f) “поднимает” (от англ. lift) обычную функцию f в мир специальных функций.
Функция lift1 у нас уже есть, это просто функция +$. Теперь давайте определим функцию lift2:
lift2 :: Kleisli m => (a -> b -> c) -> m a -> m b -> m c lift2 f a b = ...
Поскольку функция двух аргументов на самом деле является функцией одного аргумента мы можем применить первый аргумент с помощью функции lift1, посмотрим что у нас получится:
lift1 :: (a' -> b') -> m' a' -> m' b' f :: (a -> b -> c) a :: m a lift1 f a :: m (b -> c) -- m' == m, a' == a, b' == b -> c
Теперь в нашем определении для lift2 появится новое слагаемое g:
lift2 :: Kleisli m => (a -> b -> c) -> m a -> m b -> m c
lift2 f a b = ...
where g = lift1 f a
Один аргумент мы применили, осталось применить второй. Нам нужно составить выражение (g b), но для этого нам нужна функция типа:
m (b -> c) -> m b -> m c
Эта функция применяет к специальному значению функцию, которая завёрнута в тип m. Посмотрим на определение этой функции, мы назовём её $$:
($$) :: Kleisli m => m (a -> b) -> m a -> m b mf $$ ma = ( +$ ma) *$ mf
Вы можете убедиться в том, что это определение проходит проверку типов. Посмотрим как эта функция работает в интерпретаторе на примере частично определённых и многозначных функций, для этого давайте добавим в модуль Kleisli это определение и загрузим его в интерпретатор:
*Kleisli> :reload Kleisli Ok, modules loaded: Kleisli, Nat. *Kleisli> Just (+2) $$ Just 2 Just 4 *Kleisli> Nothing $$ Just 2 Nothing *Kleisli> [(+1), (+2), (+3)] $$ [10,20,30] [11,21,31,12,22,32,13,23,33] *Kleisli> [(+1), (+2), (+3)] $$ [] []
Обратите внимание на то, что в случае списков были составлены все возможные комбинации применений. Мы применили первую функцию из списка ко всем аргументам, потом вторую функцию, третью и объединили все результаты в список.
Теперь мы можем закончить наше определение для lift2:
lift2 :: Kleisli m => (a -> b -> c) -> m a -> m b -> m c
lift2 f a b = f' $$ b
where f' = lift1 f a
Мы можем записать это определение более кратко:
lift2 :: Kleisli m => (a -> b -> c) -> m a -> m b -> m c lift2 f a b = lift1 f a $$ b
Теперь давайте добавим это определение в модуль Kleisli и посмотрим в интерпретаторе как работает эта функция:
*Kleisli> :reload [2 of 2] Compiling Kleisli ( Kleisli.hs, interpreted ) Ok, modules loaded: Kleisli, Nat. *Kleisli> lift2 (+) (Just 2) (Just 2) Just 4 *Kleisli> lift2 (+) (Just 2) Nothing Nothing
Как на счёт функций трёх и более аргументов? У нас уже есть функции lift1 и lift2 определим функцию lift3:
lift3 :: Kleisli m => (a -> b -> c -> d) -> m a -> m b -> m c -> m d lift3 f a b c = ...
Первые два аргумента мы можем применить с помощью функции lift2. Посмотрим на тип получившегося выражения:
lift2 :: Kleisli m => (a' -> b' -> c') -> m a' -> m b' -> m c' f :: a -> b -> c -> d lift2 f a b :: m (c -> d) -- a' == a, b' == b, c' == c -> d
У нас опять появился тип m (c -> d) и к нему нам нужно применить значение m c, чтобы получить m d. Этим как раз и занимается функция $$. Итак итоговое определение примет вид:
lift3 :: Kleisli m => (a -> b -> c -> d) -> m a -> m b -> m c -> m d lift3 f a b c = lift2 f a b $$ c
Так мы можем определить любую функцию liftN через функции liftN-1 и $$.
Теперь мы умеем применять к специальным значениям произвольные обычные функции. Определим ещё несколько полезных функций. Первая функция принимает список специальных значений и собирает их в специальный список:
import Prelude hiding (id, (>>), pred, sequence) sequence :: Kleisli m => [m a] -> m [a] sequence = foldr (lift2 (:)) (idK [])
Мы “спрячем” из Prelude одноимённую функцию sequence. Посмотрим на примеры:
*Kleisli> sequence [Just 1, Just 2, Just 3] Just [1,2,3] *Kleisli> sequence [Just 1, Nothing, Just 3] Nothing
Во второй команде вся функция вернула Nothing потому что при объединении списка встретилось значение Nothing, это равносильно тому, что мы объединяем в один список, значения полученные из функций, которые могут не вычислить результат. Поскольку значение одного из элементов не определено, весь список не определён.
Посмотрим как работает эта функция на списках:
*Kleisli> sequence [[1,2,3], [11,22]] [[1,11],[1,22],[2,11],[2,22],[3,11],[3,22]]
Она составляет список всех комбинаций элементов из всех подсписков.
С помощью этой функции мы можем определить функцию mapK. Эта функция является аналогом обычной функции map, но она применяет специальную функцию к списку значений.
mapK :: Kleisli m => (a -> m b) -> [a] -> m [b] mapK f = sequence . map f
В этой главе мы выписали вручную все определения для класса Kleisli. Мы сделали это потому, что на самом деле в арсенале стандартных средств Haskell такого класса нет. Класс Kleisli строит замкнутый мир специальных функций a -> m b. Его цель построить язык в языке и сделать программирование со специальными функциями таким же удобным как и с обычными функциями. Мы пользовались классом Kleisli исключительно в целях облегчения понимания этого мира. Впрочем никто не мешает нам определить этот класс и пользоваться им в наших программах.
А пока посмотрим, что есть в Haskell и как это соотносится с тем, что мы уже увидели. С помощью класса Kleisli
мы научились делать три различных операции применения:
Применение:
обычных функций одного аргумента к специальным значениям (функция +$).
обычных функций произвольного числа аргументов к специальным значениям (функции +$ и $$)
специальных функций к специальным значениям (функция *$).
В Haskell для решения этих задач предназначены три отдельных класса. Это функторы, аппликативные функторы и монады.
Посмотрим на определение класса Functor:
class Functor f where
fmap :: (a -> b) -> f a -> f b
Тип метода fmap совпадает с типом для функции +$:
(+$) :: Kleisli m => (a -> b) -> m a -> m b
Нам только нужно заменить m на f и зависимость от Kleisli на зависимость от Functor:
Итак в Haskell у нас есть базовая операция fmap применения обычной функции к значению из мира специальных функций. В модуле Control.Applicative определён инфиксный синоним <$> для этой функции.
Посмотрим на определение класса Applicative:
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
Если присмотреться к типам методов этого класса, то мы заметим, что это наши старые знакомые idK и $$. Если для данного типа f определён экземпляр класса Applicative, то из контекста следует, что для него также определён и экземпляр класса Functor.
Значит у нас есть функции fmap (или lift1) и <*> (или $$). С их помощью мы можем составить функции liftN, которые поднимают обычные функции произвольного числа аргументов в мир специальных значений.
Класс Applicative определён в модуле Control.Applicative, там же мы сможем найти и функции liftA, liftA2, liftA3 и символьный синоним <$> для функции fmap. Функции liftAn определены так:
liftA2 f a b = f <$> a <*> b liftA3 f a b c = f <$> a <*> b <*> c
Видно что эти определения с точностью до обозначений совпадают с теми, что мы уже писали для класса Kleisli.
Посмотрим на определение класса Monad
class Monad m where return :: a -> m a (>>=) :: m a -> (a -> m b) -> m b
Присмотримся к типам методов этого класса:
return :: a -> m a
Их типа видно, что это ни что иное как функция idK. В классе Monad у неё точно такой же смысл. Теперь функция >>=, она читается как функция связывания (bind).
(>>=) :: m a -> (a -> m b) -> m b
Так возможно совпадение не заметно, но давайте “перевернём” эту функцию:
(=<<) :: Monad m => (a -> m b) -> m a -> m b (=<<) = flip (>>=)
Поменяв аргументы местами, мы получили знакомую функцию *$. Итак функция связывания это функция применения специальной функции к специальному значению. У неё как раз такой смысл.
В Prelude определены экземпляры класса Monad для типов Maybe и [].
Они определены по такому же принципу, что и наши определения для Kleisli только не для композиции, а для применения.
Отметим, что в модуле Control.Monad определены функции sequence и mapM, они несут тот же смысл, что и функции sequence и mapК, которые мы определяли для класса Kleisli.
Посмотрим на свойства функторов и аппликативных функторов.
fmap id x == x -- тождество fmap f . fmap g == fmap (f . g) -- композиция
Первое свойство говорит о том, что если мы применяем fmap к функции тождества, то мы должны снова получить функцию тождества, или по другому можно сказать, что применение функции тождества к специальному значению не изменяет это значение. Второе свойство говорит о том, что последовательное применение к специальному значению двух обычных функций можно записать в виде применения композиции двух обычных функций к специальному значению.
Если всё это звучит туманно, попробуем переписать эти свойства в терминах композиции:
mf +> id == mf (mf +> g) +> h == mf +> (g >> h)
Первое свойство говорит о том, что тождественная функция не изменяет значение при композиции. Второе свойство указывает на ассоциативность композиции одной специальной функции mf и двух обычных функций g и h.
Свойства класса Applicative, для наглядности они сформулированы не через методы класса, а через производные функции.
fmap f x == liftA f x -- связь с Functor liftA id x == x -- тождество liftA3 (.) f g x == f <*> (g <*> x) -- композиция liftA f (pure x) == pure (f x) -- гомоморфизм
Первое свойство говорит о том, что применение специальной функции одного аргумента совпадает с методом fmap из класса Functor. Свойство тождества идентично аналогичному свойству для класса Functor.
Свойство композиции сформулировано хитро, но давайте посмотрим на типы аргументов:
(.) :: (b -> c) -> (a -> b) -> (a -> c) f :: m (b -> c) g :: m (a -> b) x :: m a liftA3 (.) f g x :: m c g <*> x :: m b f (g <*> x) :: m c
Слева в свойстве стоит liftA3, а не liftA2, потому что мы сначала применяем композицию (.) к двум функциям f и g, а затем применяем составную функцию к значению x.
Последнее свойство говорит о том, что если мы возьмём обычную функцию и обычное значение и поднимем их в мир специальных значений с помощью lift и pure, то это тоже самое если бы мы просто применили бы функцию f к значению в мире обычных значений и затем подняли бы результат в мир специальных значений.
На самом деле я немного схитрил. Я рассказал вам только об основных методах классов Applicative и Monad. Но они содержат ещё несколько дополнительных методов, которые выражаются через остальные. Посмотрим на них, начнём с класса Applicative.
class Functor f => Applicative f where
-- | Поднимаем значение в мир специальных значений.
pure :: a -> f a
-- | Применение специального значения-функции.
(<*>) :: f (a -> b) -> f a -> f b
-- | Константная функция. Отбрасываем первое значение.
(*>) :: f a -> f b -> f b
(*>) = liftA2 (const id)
-- | Константная функция, Отбрасываем второе значение.
(<*) :: f a -> f b -> f a
(<*) = liftA2 const
Два новых метода (*>) и (<*) имеют смысл константных функций. Первая функция игнорирует значение слева, а вторая функция игнорирует значение справа. Посмотрим как они работают в интерпретаторе:
Prelude Control.Applicative> Just 2 *> Just 3 Just 3 Prelude Control.Applicative> Nothing *> Just 3 Nothing Prelude Control.Applicative> (const id) Nothing Just 3 Just 3 Prelude Control.Applicative> [1,2] <* [1,2,3] [1,1,1,2,2,2]
Значение игнорируется, но способ комбинирования специальных функций учитывается. Так во втором выражении не смотря на то, что мы не учитываем конкретное значение Nothing, мы учитываем, что если один из аргументов частично определённой функции не определён, то не определено всё значение. Сравните с результатом выполнения следующего выражения.
По той же причине в последнем выражении мы получили три копии первого списка. Так произошло потому, что второй список содержал три элемента. К каждому из элементов была применена функция const x, где x пробегает по элементам списка слева от (<*).
Аналогичный метод есть и в классе Monad:
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
fail :: String -> m a
m >> k = m >>= const k
fail s = error s
Функция >> в классе Monad, которую мы прятали из-за символа композиции, является аналогом постоянной функции в классе Monad. Она работает так же как и *>. Функция fail используется для служебных нужд Haskell при выводе ошибок. Поэтому мы её здесь не рассматриваем. Для определения экземпляра класса Monad достаточно определить методы return и >>=.
Напрашивается вопрос. Зачем нам функции return и pure или *> и >>? Если вы заглянете в документацию к модулю Control.Monad, то там вы найдёте функции liftM, liftM2, liftM3, которые выполняют те же операции, что и аналогичные функции из модуля Control.Applicative.
Стандартные библиотеки устроены так, потому что класс Applicative появился гораздо позже класса Monad. И к появлению этого нового класса уже накопилось огромное число библиотек, которые рассчитаны на прежние имена. Но в будущем возможно прежние классы будут заменены на такие классы:
class Functor f where
fmap :: (a -> b) -> f a -> f b
class Pointed f where
pure :: a -> f a
class (Functor f, Pointed f) => Applicative f where
(<*>) :: f (a -> b) -> f a -> f b
(*>) :: f a -> f b -> f b
(<*) :: f a -> f b -> f a
class Applicative f => Monad f where
(>>=) :: f a -> (a -> f b) -> f b
В этой главе мы долгой обходной дорогой шли к понятию монады и функтора. Эти классы служат для облегчения работы в мире специальных функций вида a -> m b, в категории Клейсли
С помощью класса Functor можно применять специальные значения к обычным функциям одного аргумента:
class Functor f where
fmap :: (a -> b) -> f a -> f b
С помощью класса Applicative можно применять специальные значения к обычным функциям любого числа аргументов:
class Functor f => Applicative f where
pure :: a -> f a
<*> :: f (a -> b) -> f a -> f b
liftA :: Applicative f => (a -> b) -> f a -> f b
liftA2 :: Applicative f => (a -> b -> c) -> f a -> f b -> f c
liftA3 :: Applicative f => (a -> b -> c -> d) -> f a -> f b -> f c -> f d
...
С помощью класса Monad можно применять специальные значения к специальным функциям.
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
Функция return является функцией id в мире специальных функций, а функция >>= является функцией применения ($), с обратным порядком следования аргументов. Вспомним также класс Kleisli, на примере котором мы узнали много нового из жизни специальных функций:
class Kleisli m where
idK :: a -> m a
(*>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
Мы узнали несколько стандартных специальных функций:
a -> Maybe b data Maybe a = Nothing | Just a
a -> [b] data [a] = [] | a : [a]
В первых упражнениях вам предлагается по картинке специальной функции написать экземпляр классов Kleisli и Monad.

Функция с состоянием
В Haskell нельзя изменять значения. Новые сложные значения описываются в терминах базовых значений. Но как же тогда мы сможем описать функцию с состоянием? Функцию, которая принимает на вход значение, составляет результат на основе внутреннего состояния и значения аргумента и обновляет состояние. Поскольку мы не можем изменять состояние единственное, что нам остаётся – это принимать значение состояния на вход вместе с аргументом и возвращать обновлённое состояние на выходе. У нас получится такой тип:
a -> s -> (b, s)
Функция принимает одно значение типа a и состояние типа s, а возвращает пару, которая состоит из результата типа b и обновлённого состояния. Если мы введём синоним:
type State s b = s -> (b, s)
И вспомним о частичном применении, то мы сможем записать тип функции с состоянием так:
a -> State s b
В Haskell пошли дальше и выделили для таких функций специальный тип:
data State s a = State (s -> (a, s)) runState :: State s a -> s -> (a, s) runState (State f) = f
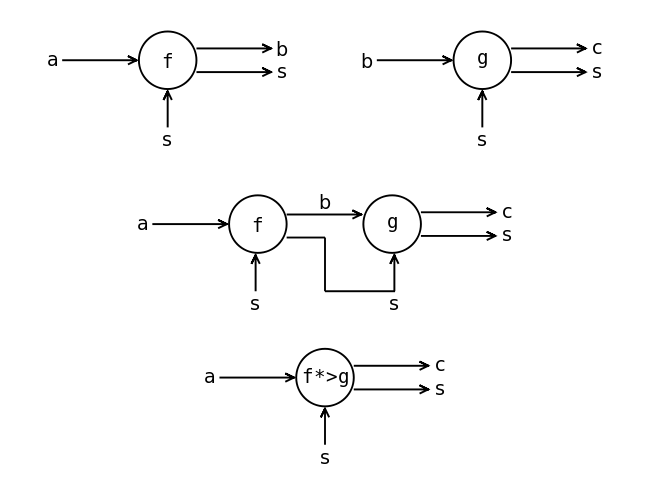
Композиция функций с состоянием
Функция runState просто извлекает функцию из оболочки State.
На рисунке изображена схема функции с состоянием. В сравнении с обычной функцией у такой функции один дополнительный выход и один дополнительный вход типа s. По ним течёт и изменяется состояние.
Попробуйте по схеме композиции для функций с состоянием написать экземпляры для классов Kleisli и Monad для типа State s.
Подсказка: В этом определении есть одна хитрость, в отличае от типов Maybe и [a] у типа State два параметра, это параметр состояния и параметр значения. Но мы делаем экземпляр не для State, а для State s, то есть мы свяжем тип с некоторым произвольным типом s.
instance Kleisli (State s) where ...
Сначала мы рассмотрим функции с окружением. Функции с окружением – это такие функции, у которых есть некоторое хранилище данных или окружение, из которых они могут читать информацию. Но в отличие от функций с состоянием они не могут это окружение изменять. Функция с окружением похожа на функцию с состоянием без одного выхода для состояния.

Функция с окружением
Функция с окружением принимает аргумент a и окружение env и возвращает результат b:
a -> env -> b
Как и в случае функций с состоянием выделим для функции с окружением отдельный тип. В Haskell он называется Reader (от англ. чтец). Все функции с окружением имеют возможность читать из общего хранилища данных. Например они могут иметь доступ на чтение к общей базе данных.
data Reader env b = Reader (env -> b) runReader :: Reader env b -> (env -> b) runReader (Reader f) = f
Теперь функция с окружением примет вид:
a -> Reader env b
Определите для функций с окружением экземпляр класса Kleisli. У нас возникнет цепочка функций, каждая из которых будет нуждаться в значении окружения. Поскольку окружение общее для всех функций мы всем функциям передадим одно и то же значение.
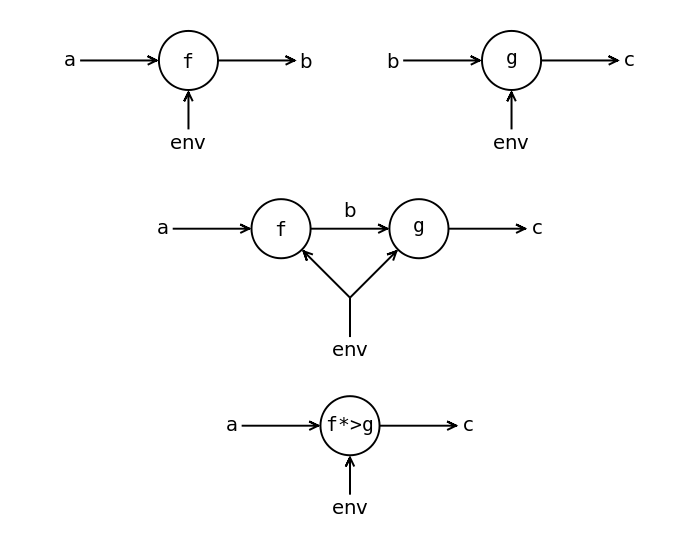
Функция с окружением
Функции-накопители при вычислении за ширмой накапливают некоторое значение. Функция-накопитель похожа на функцию с состоянием но без стрелки, по которой состояние подаётся в функцию. Функция-накопитель имеет тип: a -> (b, msg)

Функция-накопитель
Выделим результат функции в отдельный тип с именем Writer.
data Writer msg b = Writer (b, msg) runWriter :: Writer msg b -> (b, msg) runWriter (Writer a) = a
Тип функции примет вид:
a -> Writer msg b
Значения типа msg мы будем называть сообщениями. Смысл функций a -> Writer msg b заключается в том, что при вычислении они накапливают в значении msg какую-нибудь информацию. Это могут быть отладочные сообщения. Или база данных, которая открыта для всех функций на запись.
Как мы будем накапливать результат? Пока мы умеем лишь возвращать из функции пару значений. Одно из них нам нужно передать в следующую функцию, а что делать с другим?
На помощь нам придёт класс Monoid, он определён в модуле Data.Monoid:
class Monoid a where
mempty :: a
mappend :: a -> a -> a
В этом классе определено пустое значение mempty и бинарная функция соединения двух значений в одно. Этот класс очень похож на класс Category и Kleisli. Там тоже было значение, которое ничего не делает и операция составления нового значения из двух простейших значений. Даже свойства класса похожи:
mempty `mappend` f = f f `mappend` mempty = f f `mappend` (g `mappend` h) = (f `mappend` g) `mappend` h
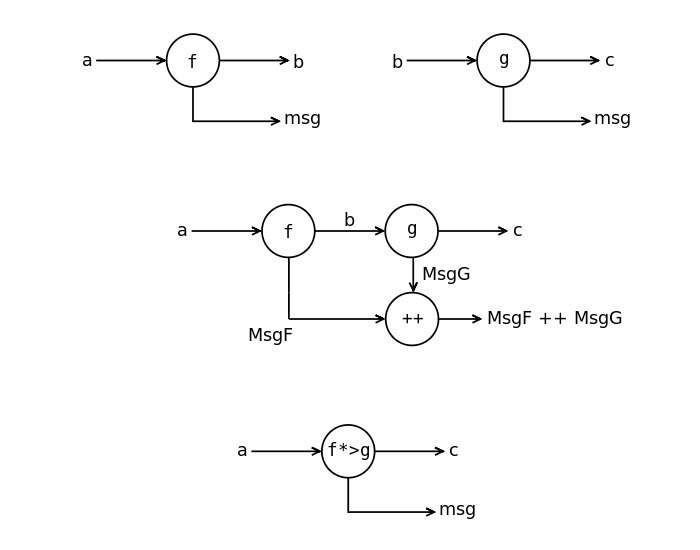
Композиция функций-накопителей
Первые два свойства говорят о том, что значение mempty и вправду является пустым элементом относительно операции mappend. А третье свойство говорит о том, что порядок при объединении элементов не важен.
Посмотрим на определение экземпляра для списков:
instance Monoid [a] where
mempty = []
mappend = (++)
Итак пустой элемент это пустой список, а объединение это операция конкатенации списков. Проверим в интерпретаторе:
*Kleisli> :m Data.Monoid Prelude Data.Monoid> [1 .. 4] `mappend` [4, 3 .. 1] [1,2,3,4,4,3,2,1] Prelude Data.Monoid> "Hello" `mappend` " World" `mappend` mempty "Hello World"
Напишите экземпляр класса Kleisli для функций накопителей по рисунку. При этом будем считать, что тип msg является экземпляром класса Monoid.
Представьте, что у нас нет класса Kleisli, а есть лишь Functor, Applicative и Monad. Напишите экземпляры для этих классов для всех рассмотренных в этой главе специальных функций (в том числе и для Reader и Writer). Экземпляры Functor и Applicative могут быть определены через Monad. Но для тренировки определите экземпляры полностью. Сначала Functor, затем Applicative и в последнюю очередь Monad.
Напишите экземпляры классов Kleisli и Monad для двух типов, которые описывают деревья. Бинарные деревья:
data BTree a = BList a | BNode a (BTree a) (BTree a)
Деревья с несколькими узлами:
data Tree a = Node a [Tree a]
Считайте, что списки являются частными случаями деревьев. В этом смысле деревья будут описывать многозначные функции, которые возвращают несколько значений, организованных в иерархическую структуру.
Почитайте документацию к модулям Control.Monad и Control.Applicative. Присмотритесь к функциям, попробуйте применить их в интерпретаторе.
Покажите, что классы Kleisli и Monad эквивалентны. Для этого нужно для произвольного типа c с одним параметром m определить два экземпляра:
instance Kleisli m => Monad m where instance Monad m => Kelisli m where
Нужно определить экземпляр одного класса с помощью методов другого.
Если класс Monad эквивалентен Kleisli, то в нём должны выполнятся точно такие же свойства. Запишите свойства класса Kleisli через методы класса Monad