
Этапы компиляции
На момент написания этой книги основным компилятором Haskell является GHC. Остальные конкуренты отстают очень сильно. Отметим компилятор Hugs (его хорошо использовать для демонстрации Haskell на чужом компьютере, если вы не хотите устанавливать тяжёлый GHC). В этой главе мы обзорно рассмотрим как язык Hаskell реализован в GHC. GHC – как ни парадоксально это звучит, это самая успешная программа написанная на Haskell. GHC уже двадцать лет. Отметим основных разработчиков. Это Саймон Пейтон Джонс (Simon Peyton Jones) и Саймон Марлоу (Simon Marlow).
GHC состоит из трёх частей. Это сам компилятор, основные библиотеки языка (такие как Prelude) и низкоуровневая система вычислений (она отвечает за управление памятью, потоками, вычисление примитивных операций). Весь GHC кроме системы вычислений написан на Haskell. Система вычислений написана на C. Компилятор принимает набор файлов с исходным кодом (а также возможно объектных и интерфейсных файлов) и генерирует код низкого уровня. Система вычислений низкого уровня используется в этом коде как библиотека. Она статически подключается к любому нативному коду, который генерируется GHC. Далее мы сосредоточимся на изучении компилятора.
Но перед этим давайте освежим в памяти (или узнаем) несколько терминов. У нас есть код на Haskell, что значит перевести в код низкого уровня? Код низкого уровня представляет собой набор инструкций, которые изменяют значения в памяти компьютера. Изменение значений происходит с помощью базовых операций, которые выполняются в процессоре компьютера. Память компьютера представляет собой ленту ячеек. У каждой ячейки есть адрес и содержание. По адресу мы можем читать данные из ячейки и записывать их туда. Эти операции также выполняются с помощью инструкций. Мы будем делить память на стек (stack), кучу (heap) и регистры (registers).
Стек – это очередь с принципом работы “последним пришёл, первым ушёл”. Стек можно представить как стопку книг. У нас есть две операции: положить книгу наверх, и снять верхнюю книгу. Стек очень удобен для переключения контекстов вычисления. Представьте, что у нас есть функция, которая внутри вызывает другую функцию, а та следующую. Находясь в верхней функции при заходе во вторую мы сохраняем контекст внешней функции в стеке. Контекст – это та информация, которая нужна нам для того, чтобы продолжить вычисления. Как только мы доходим до третьей функции, мы “кладём на стопку сверху” контекст второй функции, как только третья функция вычислена, мы обращаемся к стеку и снимаем с него контекст второй функции продолжаем вычислять и как только вторая функция заканчивается снова обращаемся к стеку. А там сверху уже лежит контекст самой первой функции. Мы можем продолжать вычисления. Так происходит вычисление вложенных функций в императивных языках программирования.
В куче мы храним разные данные. Данные бывают статическими (они нужны нам на протяжении выполнения всей программы) и динамическими (время жизни динамических данных заранее неизвестно, например это могут быть отложенные вычисления, мы не знаем когда ни нам понадобятся). У кучи также две операции: выделить блок памяти, эта операция принимает размер блока и возвращает адрес, по которому удалось выделить память, и освободить память по указанному адресу. Регистры находятся в процессоре. В них можно записывать и читать данные, при этом операции обращения к регистрам будут происходить очень быстро.
Посмотрим как GHC справляется с переводом процесса редукции синонимов на язык понятный нашему компьютеру. Язык обновления стека и кучи. Это большая и трудная глава, читайте не спеша. Если покажется совсем трудно – пропустите, вернётесь потом, когда захочется писать не только красивые, но и эффективные программы.
Рассмотрим этапы компиляции программы.

Этапы компиляции
На первых трёх этапах происходит проверка ошибок. Сначала мы строим синтаксическое дерево программы. Если мы нигде не забыли скобки, не ошиблись в простановке ключевых слов, то этот этап успешно завершится. Далее мы приписываем ко всем функциям их полные имена. Дописываем перед всеми определениями имя модуля, в котором они определены. Обычно на этом этапе нам сообщают о том, что мы забыли определить какую-нибудь функцию, часто это связано с простой опечаткой. Следующий этап – самый важный. Происходит вывод типов для всех значений и проверка программы по типам. Блок кода, отвечающий за проверку типов, является самым большим в GHC. Haskell имеет очень развитую систему типов. Многих возможностей мы ещё не коснулись, часть из них мы рассмотрим в главе 17. Допустим, что мы исправили все ошибки связанные с типами, тогда компилятор начнёт переводить Haskell в Core.
Core – это функциональный язык программирования, который является сильно урезанной версией Haskell. Помните мы говорили, что в Haskell поддерживается несколько стилей (композиционный и декларативный). Что хорошо для программиста, не очень хорошо для компилятора. Компилятор устраняет весь синтаксический сахар и выражает все определения через простейшие конструкции языка Core. Далее происходит серия оптимизаций языка Core. На дереве описания программы выполняется серия функций типа Core -> Core. Например происходит замена вызовов коротких функций на их правые части уравнений (встраивание или inlining), выражения, которые проводят декомпозицию в case-выражениях по константам, заменяются на соответствующие этим константам выражения. По требованию GHC может провести анализ строгости (strictness analysis). Он заключается в том, что GHC ищет аргументы функций, которые могут быть вычислены более эффективно с помощью вычисления по значению и расставляет аннотации строгости. И многие-многие другие оптимизации кода. Все они представлены в виде преобразования синтаксического дерева программы. Также этот этап называют упрощением программы.
После этого Core переводится на STG. Это функциональный язык, повторяющий Core. Он содержит дополнительную информацию, которая необходима низкоуровневым библиотекам на этапе вычисления программы. Затем из STG генерируется код языка C--. Это язык низкого уровня, “портируемый ассемблер”. На этом языке не пишут программы, он предназначен для автоматической генерации кода. Далее из него получают другие низкоуровневые коды. Возможна генерация C, LLVM и нативного кода (код, который исполняется операционной системой).
STG расшифровывается как Spineless Tagless G-machine. G-machine или Г-машина – это низкоуровневое описание процесса редукции графов (от Graph). Пока мы называли этот процесс редукцией синонимов. Spineless и Tagless – это термины специфичные для G-машины, которая была придумана разработчиками GHC. Tagless относится к особому представлению объектов в куче (объекты представлены единообразно, так что им не нужен специальный тег для обозначения типа объекта), а Spineless относится к тому, что в отличие от машин-предшественников, которые описывают процесс редукции графов виде последовательности инструкций, STG является небольшим функциональным языком. На представлен синтаксис языка STG. Синтаксис упрощён для чтения людьми. Несмотря на упрощения мы сможем посмотреть как происходит вычисление выражений.

Синтаксис STG
По синтаксису STG можно понять, какие выражения языка Haskell являются синтаксическим сахаром. Им просто нет места в языке STG. Например, не видим мы сопоставления с образцом. Оно как и if-выражения переписывается через case-выражения. Исчезли where-выражения. Конструкторы могут применяться только полностью, то есть для применения конструктора мы должны передать ему все аргументы. В STG let-выражения разделяют на не рекурсивные (let) и рекурсивные (letrec). Разделение проводится в целях оптимизации, мы же будем считать, что эти случаи описываются одной конструкцией.
На что стоит обратить внимание? Заметим, что функции могут принимать только атомарные значения (либо примитивные значения, либо переменные). В данном случае переменные указывают на объекты в куче. Так если в Haskell мы пишем:
foldr f (g x y) (h x)
В STG это выражение примет вид:
let gxy = THUNK (g x y)
hx = THUNK (h x)
in foldr f gxy hx
У функций появились степени. Что это? Степени указывают на арность функции, то есть на количество принимаемых аргументов. Количество принимаемых аргументов определяется по левой части функции. Поскольку в Haskell функции могут возвращать другие функции, очень часто мы не можем знать арность, тогда мы пишем $\bullet$.
Отметим два важных принципа вычисления на STG:
Новые объекты создаются в куче только в let-выражениях
Выражение приводится к СЗНФ только в case-выражениях
Выражение let a = obj in e означает добавь в кучу объект obj под именем a и затем вычисли e. Выражение case e of~{alt1;...;alt2} означает узнай конструктор в корне e и продолжи вычисления в соответствующей альтернативе. Обратите внимание на то, что сопоставления с образцом в альтернативах имеет только один уровень вложенности. Также аргумент case-выражения в отличие от функции не обязан быть атомарным.
Для тренировки перепишем на STG пример из раздела про ленивые вычисления.
data Nat = Zero | Succ Nat zero = Zero one = Succ zero two = Succ one foldNat :: a -> (a -> a) -> Nat -> a foldNat z s Zero = z foldNat z s (Succ n) = s (foldNat z s n) add a = foldNat a Succ mul a = foldNat one (add a) exp = (\x -> add (add x x) x) (add Zero two)
Теперь в STG:
data Nat = Zero | Succ Nat
zero = CON(Zero)
one = CON(Succ zero)
two = CON(Succ one)
foldNat = FUN( z s arg ->
case arg of
Zero -> z
Succ n -> let next = THUNK (foldNat z s n)
in s next
)
add = FUN( a ->
let succ = FUN( x ->
let r = CON(Succ x)
in r)
in foldNat a succ
)
mul = FUN( a ->
let succ = THUNK (add a)
in foldNat one succ
)
exp = THUNK(
let f = FUN( x -> let axx = THUNK (add x x)
in add axx x)
a = THUNK (add Zero two)
in f a
)
Программа состоит из связок вида имя = объектКучи. Эти связки называют глобальными, они становятся статическими объектами кучи, остальные объекты выделяются динамически в let-выражениях. Глобальный объект типа THUNK называют постоянной аппликативной формой (constant applicative form или сокращённо CAF).
Итак у нас есть упрощённый функциональный язык. Как мы будем вычислять выражения? Присутствие частичного применения усложняет этот процесс. Для многих функций мы не знаем заранее их арность. Так например в выражении
f x y
Функция f может иметь один аргумент в определении, но вернуть функцию. Есть два способа вычисления таких функций:
вставка-вход (push-enter). Когда мы видим применение функции, мы сначала вставляем все аргументы в стек, затем совершаем вход в тело функции. В процессе входа мы вычисляем функцию f и узнаём число аргументов, которое ей нужно, после этого мы извлекаем из стека необходимое число аргументов, и применяем к ним функцию, если мы снова получаем функцию, тогда мы опять добираем необходимое число аргументов из стека. И так пока аргументы в стеке не кончатся.
вычисление-применение (eval-apply). Вместе с функцией мы храним информацию о том, сколько аргументов ей нужно. Если это статически определённая функция (определение выписано пользователем), то число аргументов мы можем понять по левой части определения. В этой стратегии, если число аргументов известно, мы сразу вычисляем значение с нужным числом аргументов, сохранив оставшиеся в стеке, а затем извлекаем аргументы из стека и применяем к ним вычисленное значение.
Возвращаясь к исходному примеру, предположим, что арность функции f равна единице. Тогда стратегия вставка-вход сначала добавит на стек x и y, а затем будет добирать из стека необходимые аргументы. Стратегия вычисление-применение сначала вычислит (f x), сохранив y на стеке, затем попробует применить результат к y. Почему мы говорим попробует? Может так случиться, что арность значения f x окажется равным трём, но пока у нас есть лишь один аргумент, тогда мы создадим объект PAP, который соответствует частичному применению.
Эти стратегии применимы как к ленивым, так и к энергичным языкам. Исторически сложилось, что ленивые языки тяготеют к первой стратегии, а энергичные ко второй. До недавнего времени и в GHC применялась первая стратегия. Пока однажды разработчики GHC всё же не решили сравнить две стратегии. Реализовав обе стратегии, и проверив их на большом количестве разных по сложности программ, они пришли к выводу, что ни одна из стратегий не даёт существенного преимущества на этапе вычислений. Потребление ресурсов оказалось примерно равным. Но вторая стратегия заметно выигрывала в простоте реализации. Подробнее об этом можно почитать в статье Simon Marlow, Simon Peyton Jones: Making a Fast Curry: Push/Enter vs. Eval/Apply. Описание модели вычислений GHC, которое вы сейчас читаете копирует описание приведённое в этой статье.
Объекты кучи принято называть замыканиями (closure). Их называют так, потому что обычно для вычисления выражения нам не достаточно знать его текст, например посмотрим на функцию:
mul = FUN( a ->
let succ = THUNK (add a)
in foldNat one succ
)
Для того, чтобы вычислить THUNK(add a) нам необходимо знать значение a, это значение определено в теле функции. Оно определяется из контекста. По отношению к объекту такую переменную называют свободной (free). В куче мы будем хранить не только выражение (add a), но и ссылки на все свободные переменные, которые участвуют в выражении объекта. Эти ссылки называют довесок (payload). Объект кучи содержит ссылку на специальную таблицу и довесок. В таблице находятся информация о типе объекта и код, который необходимо вычислить, а также другая служебная информация. При вычислении объекта мы заменяем ссылки настоящими значениями или ссылками на конструкторы.
Объект кучи может быть:
FUN – определением функции;PAP – частичным применением;CON – полностью применённым конструктором;THUNK – отложенным вычислением;BLACKHOLE – это значение используется во время вычисления THUNK. Этот трюк предотвращает появление утечек памяти.Мы будем считать, что куча – это таблица, которая ставит в соответствие адресам объекты или вычисленные значения.
Стек служит для быстрого переключения контекста. Мы будем пользоваться стеком при вычислении case-выражений и THUNK-объектов. При вычислении case-выражения мы сохраняем в стеке альтернативы и место возврата значения, а сами начинаем вычислять аргумент case-выражения. При вычислении THUNK-объекта мы запомним в стеке, адрес с которым необходимо связать полученное значение.
При вычислении в стратегии вставка-вход мы будем сохранять в стеке аргументы функции. А при вычислении в стратегии вычисление-применение мы также будем сохранять аргументы функции в стеке. Какая разница между этими вариантами? В первой стратегии мы можем доставать из стека произвольное число аргументов, после определения арности функции мы добираем столько, сколько нам нужно, поэтому мы будем хранить аргументы по одному. Во второй же стратегии нам нужно просто сохранить все оставшиеся аргументы. Мы сохраняем и извлекаем их все сразу. Упрощая, объекты стека можно представить так:
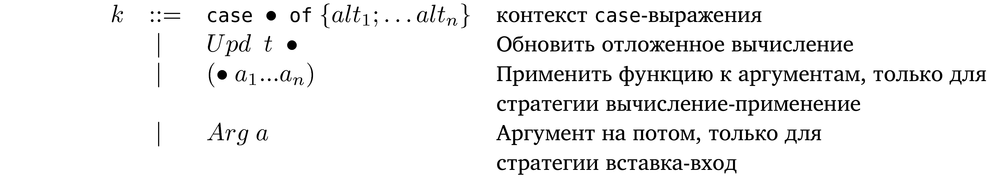
Синтаксис STG
Состояние вычислителя состоит из трёх частей. Это выражение для вычисления $e$, стек $s$ и куча $H$. Мы рассмотрим правила по которым вычислитель переходит из одного состояния в другое. Все они имеют вид:
$e_1;\quad s_1;\quad H_1\quad \Rightarrow\quad e_2;\quad s_2;\quad H_2$
Левая часть переходит в правую, при условии, что левая часть имеет определённый вид. Начнём с правил, которые одинаковы и в той и в другой стратегии вычисления. Для простоты пока мы будем полагать, что объекты только добавляются в кучу и никогда не стираются. Мы будем обозначать добавление в стек как добавление элемента в обычный список: $elem\ :\ s$.
Рассмотрим правило для let-выражений:

Синтаксис STG
В этом правиле мы добавляем в кучу новый объект $obj$ под именем (или по адресу) $x'$. Запись $e[x'/x]$ означает замену $x$ на $x'$ в выражении $e$.
Теперь разберёмся с правилами для case-выражений.
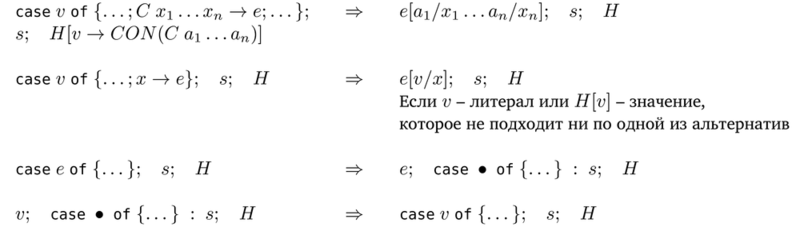
Синтаксис STG
Вычисления начинаются с третьего правила, в котором нам встречается case-выражения с произвольным $e$. В этом правиле мы сохраняем в стеке альтернативы и адрес возвращаемого значения и продолжаем вычисление выражения $e$. После вычисления мы перейдём к четвёртому правилу, тогда мы снимем со стека информацию необходимую для продолжения вычисления case-выражения. Это приведёт нас к одному из первых двух правил. В первом правиле значение аргумента содержит конструктор, подходящий по одной из альтернатив, а во втором мы выбираем альтернативу по умолчанию.
Теперь посмотрим как вычисляются THUNK-объекты.
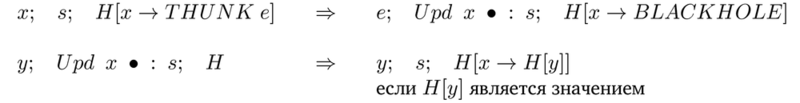
Синтаксис STG
Если переменная указывает на отложенное вычисление $e$, мы сохраняем в стеке адрес по которому необходимо обновить значение и вычисляем значение $e$. В это время мы записываем в по адресу $x$ объект $BLACKHOLE$. У нас нет такого правила, которое реагирует на левую часть, если в ней содержится объект $BLACKHOLE$. Поэтому во время вычисления $THUNK$ ни одно из правил сработать не может. Этот трюк необходим для избежания утечек памяти. Как только выражение будет вычислено, мы извлечём из стека адрес $x$ и обновим значение.
Правила применения функций, если арность совпадает с числом аргументов в тексте выражения:

Синтаксис STG
Мы просто заменяем все вхождения аргументов на значения. Второе правило выполняет применение примитивной функции к значениям.

Синтаксис STG
Первое правило выполняет этап “вставка”. Если мы видим применение функции, мы первым делом сохраняем все аргументы в стеке. Во втором правиле мы вычислили значение f, оно оказалось функцией с арностью $n$. Тогда мы добираем из стека $n$ аргументов и подставляем их в правую часть функции $e$. Если в стеке оказалось слишком мало аргументов, то мы переходим к третьему правилу и составляем частичное применение. Последнее правило говорит о том как расшифровывается частичное применение. Мы вставляем в стек все аргументы и начинаем вычисление функции $g$ из тела $PAP$.

Синтаксис STG
Разберёмся с первыми двумя правилами. В первом правиле статическая арность $f$ неизвестна, но значение $f$ уже вычислено, и мы можем узнать арность по объекту $FUN$, далее возможны три случая. Число аргументов переданных в функцию совпадает с арностью $FUN$, тогда мы применяем аргументы к правой части $FUN$. Если в функцию передано больше аргументов чем нужно, мы сохраняем лишние на стеке. Если же аргументов меньше, то мы создаём объект $PAP$. Третье правило говорит о том, что нам делать, если значение $f$ ещё не вычислено. Оно является $THUNK$. Тогда мы сохраним аргументы на стеке и вычислим его. В следующем правиле мы раскрываем частичное применение. Мы просто организуем вызов функции со всеми аргументами (и со стека и из частичного применения). Последнее правило срабатывает после третьего. Когда мы вычислим $THUNK$ и увидим там $FUN$ или $PAP$. Тогда мы составляем применение функции.
Сложность применения стратегии вставка-вход связана с плохо предсказуемым изменением стека. Если в стратегии вычисление-выполнение мы добавляем и снимаем все аргументы, то в стратегии вставка-вход мы добавляем их по одному и неизвестно сколько снимем в следующий раз. Кроме того стратегия вычисление-применение позволяет проводить оптимизацию перемещения аргументов. Вместо стека мы можем хранить аргументы в регистрах. Тогда скорость обращения к аргументам резко возрастёт.
Ранее мы говорили, что полностью вычисленное значение – это дерево, в узлах которого находятся одни лишь конструкторы. Процесс вычисления похож на очистку дерева выражения от синонимов. Мы начинаем с самого верха и идём к листьям. Потом мы выяснили, что для предотвращения дублирования вычислений мы подставляем в функции не сами значения, а ссылки на значения. Теперь нам понятно, что ссылки указывают на объекты в куче. Ссылки – это атомарные переменные. Полностью вычисленное значение является сетью (или графом) объектов кучи типа CON.
Поговорим о том сколько места в памяти занимает то или иное значение. Как мы говорили память компьютера состоит из ячеек, в которых хранятся значения. У каждой ячейки есть адрес. Ячейки памяти неделимы, их также принято называть словами. Мы будем оценивать размер значения в словах.
Каждый конструктор требует столько слов сколько у него полей плюс ещё одно слово для ссылки на служебную информацию (она нужна вычислителю). Посмотрим на примеры:
data Int = I# Int# -- 2 слова data Pair a b = Pair a b -- 3 слова
У этого правила есть исключение. Если у конструктора нет полей, то есть он является константой или примитивным конструктором, то в процессе вычисления значение этого конструктора представлено ссылкой. Это означает, что внутри программы все значения ссылаются на одну область памяти. У нас действительно есть лишь один пустой список или одно значение True или False.
Посчитаем число слов в значении [Pair 1 2]. Для этого для начала перепишем его в STG
nil = [] -- глобальный объект (не в счёт)
let x1 = I# 1 -- 2 слова
x2 = I# 2 -- 2 слова
p = Pair x1 x2 -- 3 слова
val = Cons p nil -- 3 слова
in val ------------
-- 10 слов
Поскольку объект кучи CON может хранить только ссылки, нам пришлось введением дополнительных переменных “развернуть” значение. Примитивный конструктор не считается, поскольку он сохранён глобально, в итоге получилось 10 слов. Посмотрим на ещё один пример, распишем значение [Just True, Just True, Nothing]:
nil = []
true = True
nothing = Nothing
let x1 = Just true -- 2 слова
x2 = Just true -- 2 слова
p1 = Cons nothing nil -- 3 слова
p2 = Cons x2 p1 -- 3 слова
p3 = Cons x1 p2 -- 3 слова
in p3 ----------
-- 13 слов
Обычно одно слово соответствует 16, 32 или 64 битам. Эта цифра зависит от процессора. Мы считали, что любое значение можно поместить в одно слово, но это не так. Возьмём к примеру действительные числа с двойной точностью, они не поместятся в одно слово. Это необходимо учитывать при оценке объёма занимаемой памяти.
В прошлом разделе для простоты мы считали, что объекты только добавляются в кучу. На самом деле это не так. Допустим во время вычисления функции нам нужно было вычислить какие-то промежуточные данные, например объявленные в локальных переменных, тогда после вычисления результата все эти значения больше не нужны. При этом в куче висит много-много объектов, которые уже не нужны. Нам нужно как-то от них избавится. Этой задачей занимается отдельный блок вычислителя, который называется сборщиком мусора (garbage collector), соответственно процесс автоматического освобождения памяти называется сборкой мусора (garbage collection или GC).
На данный момент в GHC используется копирующий последовательный сборщик мусора, который работает по алгоритму Чейни (Cheney). Для начала рассмотрим простой алгоритм сборки мусора. Мы выделяем небольшой объём памяти и начинаем наполнять его объектами. Как только место кончится мы найдём все “живые” объекты, а остальное пространство памяти будем считать свободным. Как только после очередной очистки оказалось, что нам всё же не хватает места. Мы найдём все живые объекты, подсчитаем сколько места они занимают и запросим у системы этот объём памяти. Скопируем все живые объекты на новое место, а старую память будем считать свободной. Так например, если у нас было выделено 30 Мб памяти и оказалось, что живые объекты занимают 10 Мб, мы выделим ещё 10 Мб, скопируем туда все живые объекты и общий объём памяти станет равным 40 Мб.
Мы можем оптимизировать сборку мусора. Есть такая гипотеза, что большинство объектов имеют очень короткую жизнь. Это промежуточные данные, локальные переменные. Нам нужен лишь результат функции, но на подходе к результату мы сгенерируем много разовой информации. Ускорить очистку можно так. Мы выделим совсем небольшой участок памяти внутри нашей кучи, его принято называть яслями (nursery area), и будем выделять и собирать новые объекты только в нём, как только этот участок заполнится мы скопируем все живые объекты из яслей в остальную память и снова будем наполнять ясли. Как только вся память закончится мы поступим так же как и в предыдущем сценарии. Когда заканчивается место в яслях, мы проводим поверхностную очистку (minor GC), а когда заканчивается вся память в текущей куче, мы проводим глубокую очистку (major GC). Эта схема соответствует сборке с двумя поколениями.
Процесс управления памятью скрыт от программиста. Но при этом в GHC есть развитые средства косвенной диагностики работы программы. Пока мы пользовались самым простым способом проверки. Мы включали флаг s в интерпретаторе. Пришло время познакомиться и с другими.
Для начала научимся смотреть статистику работы вычислителя. Посмотреть статистику можно с помощью флагов s[file] и S[file]. Эти флаги предназначены для вычислителя низкого уровня (realtime system или RTS, далее просто вычислитель), они заключаются в окружение +RTS ... -RTS, если флаги идут в конце строки и считается, что все последующие флаги предназначены для RTS мы можем просто написать ghc --make file.hs +RTS ... Например скомпилируем такую программу:
module Main where main = print $ sum [1 .. 1e5]
Теперь скомпилируем:
$ ghc --make sum.hs -rtsopts -fforce-recomp
Флаг rtsopts позволяет передавать скомпилированной программе флаги для вычислителя низкого уровня, далее для краткости мы будем называть его просто вычислителем. С флагом fforce-recomp программа будет каждый раз заново пересобираться. Теперь посмотрим на статистику выполнения программы (флаг s[file], в этом примере мы перенаправляем выход в поток stderr):
$ ./sum +RTS -sstderr
5.00005e9
14,145,284 bytes allocated in the heap
11,110,432 bytes copied during GC
2,865,704 bytes maximum residency (3 sample(s))
460,248 bytes maximum slop
7 MB total memory in use (0 MB lost due to fragmentation)
Tot time (elapsed) Avg pause Max pause
Gen 0 21 colls, 0 par 0.00s 0.01s 0.0006s 0.0036s
Gen 1 3 colls, 0 par 0.01s 0.01s 0.0026s 0.0051s
INIT time 0.00s ( 0.00s elapsed)
MUT time 0.01s ( 0.01s elapsed)
GC time 0.01s ( 0.02s elapsed)
EXIT time 0.00s ( 0.00s elapsed)
Total time 0.02s ( 0.03s elapsed)
%GC time 60.0% (69.5% elapsed)
Alloc rate 1,767,939,507 bytes per MUT second
Productivity 40.0% of total user, 26.0% of total elapsed
Был распечатан результат и отчёт о работе программы. Разберёмся с показателями:
bytes allocated in the heap -- число байтов выделенных в куче
-- за всё время работы программы
bytes copied during GC -- число скопированных байтов
-- за всё время работы программы
bytes maximum residency -- в каком объёме памяти работала программа
-- в скобках указано число глубоких очисток
bytes maximum slop -- максимум потерь памяти из-за фрагментации
total memory in use -- сколько всего памяти было запрошено у ОС
Показатель bytes maximum residency измеряется только при глубокой очистке, поскольку новая память выделяется именно в этот момент. Размер памяти выделенной в куче гораздо больше общего объёма памяти. Так происходит потому, что этот показатель указывает на общее число памяти в куче за всё время работы программы. Ведь мы переиспользуем не нужную нам память. По этому показателю можно судить о том, сколько замыканий (объектов) было выделено в куче.
Следующие две строчки говорят о числе сборок мусора. Мы видим, что GC выполнил 21 поверхностную очистку (поколение 0) и 3 глубоких (поколение 1). Дальше идут показатели скорости. INIT и EXIT – это инициализация и завершение программы. MUT – это полезная нагрузка, время, которая наша программа тратила на изменение (MUTation) значений. GC – время сборки мусора. Далее GHC сообщил нам о том, что мы провели 60% времени в сборке мусора. Это очень плохо. Продуктивность программы очень низкая. Затратна глубокая сборка мусора, поверхностная – это дело обычное. Теперь посмотрим на показатели строгой версии этой программы:
module Main where import Data.List(foldl') sum' = foldl' (+) 0 main = print $ sum' [1 .. 1e5]
Скомпилируем:
$ ghc --make sumStrict.hs -rtsopts -fforce-recomp
Посмотрим на статистику:
$ ./sumStrict +RTS -sstderr
5.00005e9
10,474,128 bytes allocated in the heap
24,324 bytes copied during GC
27,072 bytes maximum residency (1 sample(s))
27,388 bytes maximum slop
1 MB total memory in use (0 MB lost due to fragmentation)
Tot time (elapsed) Avg pause Max pause
Gen 0 19 colls, 0 par 0.00s 0.00s 0.0000s 0.0000s
Gen 1 1 colls, 0 par 0.00s 0.00s 0.0001s 0.0001s
INIT time 0.00s ( 0.00s elapsed)
MUT time 0.01s ( 0.01s elapsed)
GC time 0.00s ( 0.00s elapsed)
EXIT time 0.00s ( 0.00s elapsed)
Total time 0.01s ( 0.01s elapsed)
%GC time 0.0% (3.0% elapsed)
Alloc rate 1,309,266,000 bytes per MUT second
Productivity 100.0% of total user, 116.0% of total elapsed
Мы видим, что произошла лишь одна глубокая сборка. И это существенно сказалось на продуктивности. Кромке того мы видим, что программа заняла лишь 27 Кб памяти, вместо 2 Мб как в прошлом случае. Теперь давайте покрутим ручки у GC. В GHC можно устанавливать разные параметры сборки мусора с помощью флагов. Все флаги можно посмотреть в документации GHC. Мы обратим внимание на несколько флагов. Флаг H назначает минимальное значение для стартового объёма кучи. Флаг A назначает объём памяти для яслей. По умолчанию размер яслей равен 512 Кб (эта цифра может измениться). Изменением этих параметров мы можем отдалить сборку мусора. Чем дольше работает программа между сборками, тем выше вероятность того, что многие объекты уже не нужны.
Давайте убедимся в том, что поверхностные очистки происходят очень быстро и совсем не тормозят программу. Установим размер яслей на 32 Кб вместо 512 Кб как по умолчанию (размер пишется сразу за флагом, за цифрой идёт k или m):
$ ./sumStrict +RTS -A32k -sstderr
...
Tot time (elapsed) Avg pause Max pause
Gen 0 318 colls, 0 par 0.00s 0.00s 0.0000s 0.0000s
Gen 1 1 colls, 0 par 0.00s 0.00s 0.0001s 0.0001s
...
MUT time 0.01s ( 0.01s elapsed)
GC time 0.00s ( 0.00s elapsed)
...
%GC time 0.0% (11.8% elapsed)
Мы видим, что за счёт уменьшения памяти очистки существенно участились, но это не сказалось на общем результате. С помощью флага H[size] мы можем устанавливать рекомендуемое минимальное значение для размера кучи. Оно точно не будет меньше. Вернёмся к первому варианту и выделим алгоритму побольше памяти, например 20 Мб:
./sum +RTS -A1m -H20m -sstderr
5.00005e9
14,145,284 bytes allocated in the heap
319,716 bytes copied during GC
324,136 bytes maximum residency (1 sample(s))
60,888 bytes maximum slop
22 MB total memory in use (1 MB lost due to fragmentation)
Tot time (elapsed) Avg pause Max pause
Gen 0 2 colls, 0 par 0.00s 0.00s 0.0001s 0.0001s
Gen 1 1 colls, 0 par 0.00s 0.00s 0.0007s 0.0007s
INIT time 0.00s ( 0.00s elapsed)
MUT time 0.02s ( 0.02s elapsed)
GC time 0.00s ( 0.00s elapsed)
EXIT time 0.00s ( 0.00s elapsed)
Total time 0.02s ( 0.02s elapsed)
%GC time 0.0% (4.4% elapsed)
Alloc rate 884,024,998 bytes per MUT second
Productivity 100.0% of total user, 78.6% of total elapsed
Произошла лишь одна глубокая очистка (похоже, что эта очистка соответствует начальному выделению памяти) и продуктивность программы стала стопроцентной. С помощью флага S вместо s мы можем посмотреть более детальную картину управления памяти. Будут распечатаны показатели памяти для каждой очистки.
./sum +RTS -Sfile
В файле file мы найдём такую таблицу:
память время выделено скопировано в живых GC Total Тип очистки Alloc Copied Live GC GC TOT TOT Page Flts bytes bytes bytes user elap user elap 545028 150088 174632 0.00 0.00 0.00 0.00 0 0 (Gen: 1) 523264 298956 324136 0.00 0.00 0.00 0.00 0 0 (Gen: 0) ...
Итак у нас появился один существенный показатель качества программ. Это количество глубоких очисток. Во время глубокой очистки вычислитель производит две затратные операции: сканирование всей кучи и запрос у системы возможно большого блока памяти. Чем меньше таких очисток, тем лучше. Сократить их число можно удачной комбинацией показателей A и H. Но не стоит сразу начинать обновлять параметры по умолчанию, если ваша программа работает слишком медленно. Лучше сначала попробовать изменить алгоритм. Найти функцию, которая слишком много ленится и ограничить её с помощью seq или энергичных образцов. В этом примере у нас была всего одна функция, поэтому поиск не составил труда. Но что если их уже очень много? Скорее всего так и будет. Не стоит оптимизировать не рабочую программу. А в рабочей программе обычно много функций. Но это не так страшно, помимо суммарных показателей GHC позволяет собирать более конкретную статистику.
Стоит отметить функцию performGC из модуля System.Mem, она форсирует поверхностную сборку мусора. Допустим вы читаете какие-то данные из файла и тут же преобразуете их в структуру данных. После того как чтение данных закончится, вы знаете, что промежуточные данные, связанные с чтением, вам уже не нужны. Выполнив performGC вы можете подсказать об этом вычислителю.
Процесс отслеживания показателей память/скорость называется профилированием программы. Всё вроде бы работает, но работает слишком медленно, необходимо установить причину. Рассмотрим такую программу:
module Main where
concatR = foldr (++) []
concatL = foldl (++) []
fun :: Double
fun = test concatL - test concatR
where test f = last $ f $ map return [1 .. 1e6]
main = print fun
У нас есть подозрение, что какая-то из двух функций concatX работает слишком медленно. Мы можем посмотреть какая, если добавим к ним специальную прагму SCC:
concatR = {-# SCC "right" #-} foldr (++) []
concatL = {-# SCC "left" #-} foldl (++) []
Напомню, что прагмой называется специальный блочный комментарий с решёткой. Это специальное сообщение компилятору. Прагмой SCC мы устанавливаем так называемый центр затрат (cost center). Она пишется сразу за знаком равно. В кавычках пишется имя, под которым статистика войдёт в итоговый отчёт. После этого вычислитель будет следить за нагрузкой, которая приходится на эту функцию. Теперь нам нужно скомпилировать модуль с флагом prof, который активирует подсчёт статистики в центрах затрат:
$ ghc --make concat.hs -rtsopts -prof -fforce-recomp $ ./concat +RTS -p
Второй командой мы запускаем программу и передаём вычислителю флаг p. После этого будет создан файл concat.prof. Откроем этот файл:
concat +RTS -p -RTS
total time = 1.45 secs (1454 ticks @ 1000 us, 1 processor)
total alloc = 1,403,506,324 bytes (excludes profiling overheads)
COST CENTRE MODULE %time %alloc
left Main 99.8 99.8
individual inherited
COST CENTRE MODULE no. entries %time %alloc %time %alloc
MAIN MAIN 46 0 0.0 0.0 100.0 100.0
CAF GHC.Integer.Logarithms.Internals 91 0 0.0 0.0 0.0 0.0
CAF GHC.IO.Encoding.Iconv 71 0 0.0 0.0 0.0 0.0
CAF GHC.IO.Encoding 70 0 0.0 0.0 0.0 0.0
CAF GHC.IO.Handle.FD 57 0 0.0 0.0 0.0 0.0
CAF GHC.Conc.Signal 56 0 0.0 0.0 0.0 0.0
CAF Main 53 0 0.2 0.2 100.0 100.0
right Main 93 1 0.0 0.0 0.0 0.0
left Main 92 1 99.8 99.8 99.8 99.8
Мы видим, что почти всё время работы программа провела в функции concatL. Функция concatR была вычислена мгновенно (time) и почти не потребовала ресусов памяти (alloc). У нас есть две пары колонок результатов. individual указывает на время вычисления функции, а inherited – на время вычисления функции и всех дочерних функций. Колонка entries указывает число вызовов функции. Если мы хотим проверить все функции мы можем не указывать функции прагмами. Для этого при компиляции указывается флаг auto-all. Отметим также, что все константы определённый на самом верхнем уровне модуля, сливаются в один центр. Они называются в отчёте как CAF. Для того чтобы вычислитель следил за каждой константой по отдельности необходимо указать флаг caf-all. Попробуем на таком модуле:
module Main where fun1 = test concatL - test concatR fun2 = test concatL + test concatR test f = last $ f $ map return [1 .. 1e4] concatR = foldr (++) [] concatL = foldl (++) [] main = print fun1 >> print fun2
Скомпилируем:
$ ghc --make concat2.hs -rtsopts -prof -auto-all -caf-all -fforce-recomp $ ./concat2 +RTS -p 0.0 20000.0
После этого можно открыть файл concat2.prof и посмотреть итоговую статистику по всем значениям. Программа с включённым профилированием будет работать гораздо медленней, не исключено, что ей не хватит памяти на стеке, в этом случае вы можете добавить памяти с помощью флага вычислителя K, впрочем если это произойдёт GHC подскажет вам что делать.
В предыдущем разделе мы смотрели общее время и память затраченные на вычисление функции. В этом мы научимся измерять динамику изменения расхода памяти на куче. По этому показателю можно понять в какой момент в программе возникают утечки памяти. Мы увидим характерные горбы на картинках, когда GC будет активно запрашивать новую память. Для этого сначала нужно скомпилировать программу с флагом prof как и в предыдущем разделе, а при выполнении программы добавить один из флагов hc, hm, hd, hy или hr. Все они начинаются с буквы h, от слова heap (куча). Вторая буква указывает тип графика, какими показателями мы интересуемся. Все они создают специальный файл имяПриложения.hp, который мы можем преобразовать в график в формате PostScript с помощью программы hp2ps, она устанавливается автоматически вместе с GHC.
Рассмотрим типичную утечку памяти (из упражнения к предыдущей главе):
module Main where
import System.Environment(getArgs)
main = print . sum2 . xs . read =<< fmap head getArgs
where xs n = [1 .. 10 ^ n]
sum2 :: [Int] -> (Int, Int)
sum2 = iter (0, 0)
where iter c [] = c
iter c (x:xs) = iter (tick x c) xs
tick :: Int -> (Int, Int) -> (Int, Int)
tick x (c0, c1) | even x = (c0, c1 + 1)
| otherwise = (c0 + 1, c1)
Скомпилируем с флагом профилирования:
$ ghc --make leak.hs -rtsopts -prof -auto-all
Статистика вычислителя показывает, что эта программа вызывала глубокую очистку 8 раз и выполняла полезную работу лишь 40% времени.
$ ./leak 6 +RTS -K30m -sstderr
...
Tot time (elapsed) Avg pause Max pause
Gen 0 493 colls, 0 par 0.26s 0.26s 0.0005s 0.0389s
Gen 1 8 colls, 0 par 0.14s 0.20s 0.0248s 0.0836s
...
Productivity 40.5% of total user, 35.6% of total elapsed
Теперь посмотрим на профиль кучи.
$ ./leak 6 +RTS -K30m -hc (500000,500000) $ hp2ps -e80mm -c leak.hp
В первой команде мы добавили флаг hc для того, чтобы создать файл с расширением .hp. Он содержит таблицу с показателями размера кучи, которые вычислитель замеряет через равные промежутки времени. Мы можем изменять интервал с помощью флага iN, где N – время в секундах. Второй командой мы преобразуем профиль в картинку. Флаг c, говорит о том, что мы хотим получить цветную картинку, а флаг e80mm, говорит о том, что мы собираемся вставить картинку в текст LaTeX. После e указан размер в миллиметрах. Мы видим характерный горб.
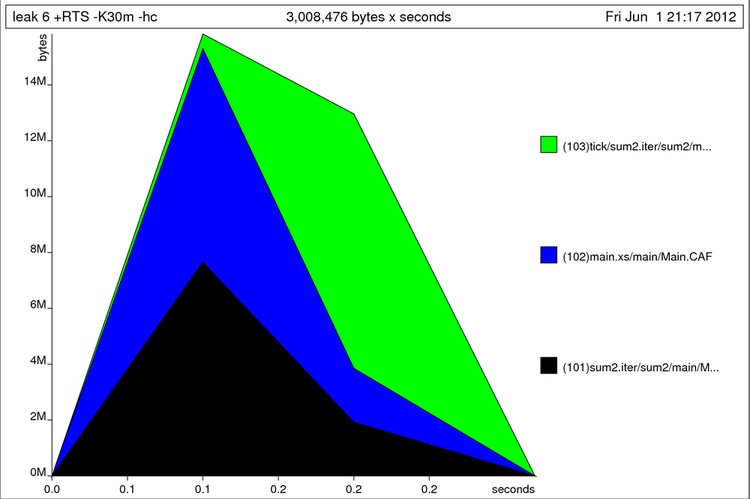
Профиль кучи для утечки памяти
В картинку не поместились имена функций мы можем увеличить строку флагом L. Теперь все имена поместились.
$ ./leak 6 +RTS -K30m -hc -L45 (500000,500000) $ hp2ps -e80mm -c leak.hp
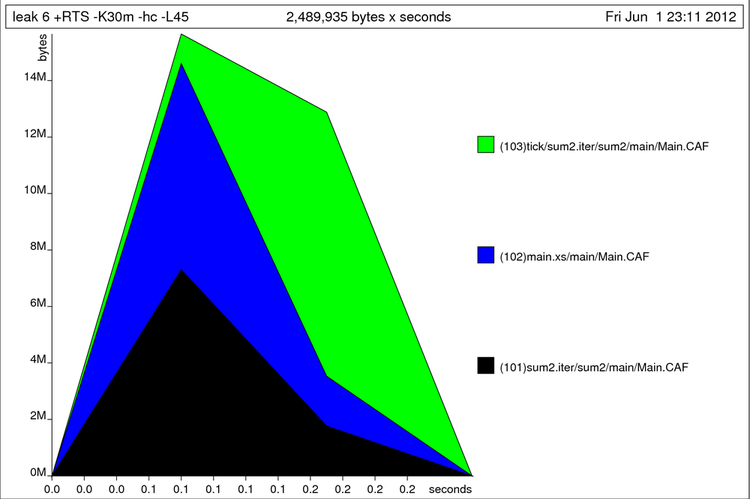
Профиль кучи для утечки памяти
С помощью флага hd посмотрим на объекты, которые застряли в куче:
$ ./leak 6 +RTS -K30m -hd -L45 (500000,500000) $ hp2ps -e80mm -c leak.hp
Теперь куча разбита по типу объектов (замыканий). BLACKHOLE это специальный объект, который заменяет THUNK во время его вычисления. I# – это скрытый конструктор Int. sat_sUa и sat_sUd – это имена застрявших отложенных вычислений. Если бы наша программа была очень большой на этом месте мы бы запустили профилирование по функциям с флагом p и из файла leak.prof узнали бы в каких функциях программа тратит больше всего ресурсов. После этого мы бы пошли смотреть исходный код подозрительных функций и после внесённых изменений снова посмотрели бы на графики кучи.
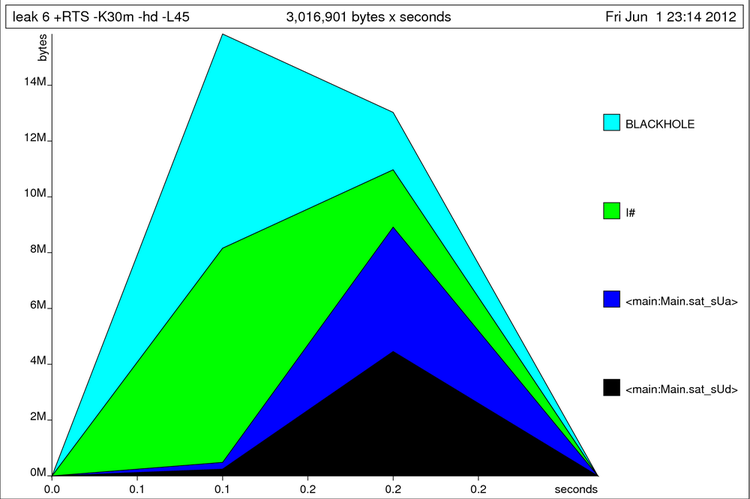
Профиль кучи для утечки памяти
Если подумать, что мы делаем? Мы создаём отложенное вычисление, которое обещает построить большой список, вытягиваем из списка по одному элементу и, если элемент оказывается чётным, прибавляем к одному элементу пары, а если не чётным, то к другому. Проблема в том, что внутри пары происходит накопление отложенных вычислений, необходимо сразу вычислять значения перед запаковыванием их в пару. Изменим код:
{-# Language BangPatterns #-}
module Main where
import System.Environment(getArgs)
main = print . sum2 . xs . read =<< fmap head getArgs
where xs n = [1 .. 10 ^ n]
sum2 :: [Int] -> (Int, Int)
sum2 = iter (0, 0)
where iter c [] = c
iter c (x:xs) = iter (tick x c) xs
tick :: Int -> (Int, Int) -> (Int, Int)
tick x (!c0, !c1) | even x = (c0, c1 + 1)
| otherwise = (c0 + 1, c1)
Мы сделали функцию tick строгой. Теперь посмотрим на профиль:
$ ghc --make leak2.hs -rtsopts -prof -auto-all $ ./leak2 6 +RTS -K30m -hc (500000,500000) $ hp2ps -e80mm -c leak2.hp
Не получилось. Как же так. Посмотрим на расход памяти отдельных функций. tick стала строгой, но этого не достаточно, потому что в первом аргументе iter накапливаются вызовы tick. Сделаем iter строгой по первому аргументу:
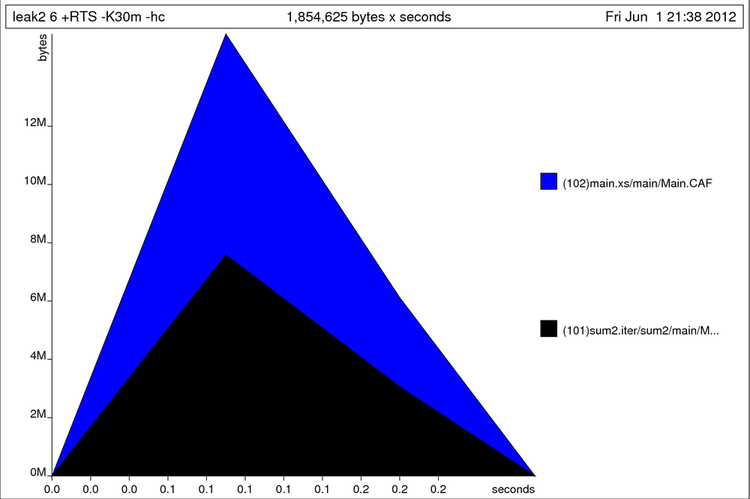
Опять двойка
sum2 :: [Int] -> (Int, Int)
sum2 = iter (0, 0)
where iter !c [] = c
iter !c (x:xs) = iter (tick x c) xs
Теперь снова посмотрим на профиль:
$ ghc --make leak2.hs -rtsopts -prof -auto-all $ ./leak2 6 +RTS -K30m -hc (500000,500000) $ hp2ps -e80mm -c leak2.hp
Мы видим, что память резко подскакивает и остаётся постоянной. Но теперь показатели измеряются не в мегабайтах, а в килобайтах. Мы справились. Остальные флаги hX позволяют наблюдать за разными специфическими объектами в куче. Мы можем узнать сколько памяти приходится на разные модули (hm), сколько памяти приходится на разные конструкторы (hd), на разные типы замыканий (hy).
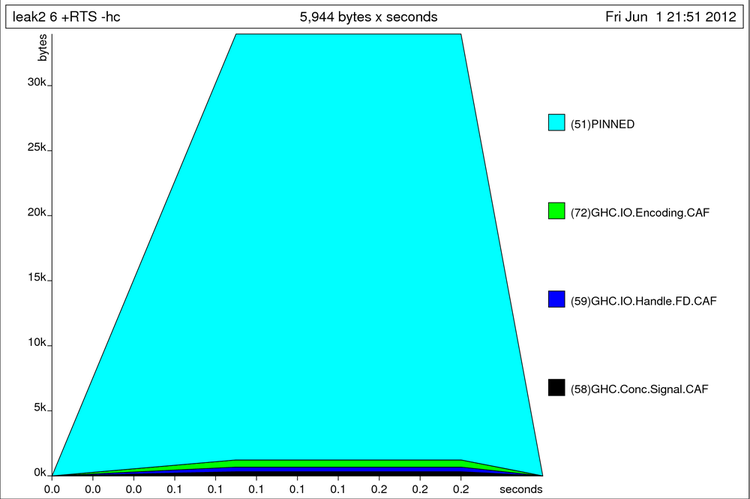
Профиль кучи без утечки памяти
case-выражения и декомпозиция в аргументах функции могут стать источником очень неприятных ошибок. Программа прошла проверку типов, завелась и вот уже работает-работает как вдруг мы видим на экране:
*** Exception: Prelude.head: empty list
или
*** Exception: Maybe.fromJust: Nothing
И совсем не понятно откуда эта ошибка. В каком модуле сидит эта функция. Может мы её импортировали из чужой библиотеки или написали сами. Как раз для таких случаев в GHC предусмотрен специальный флаг xc.
Посмотрим на выполнение такой программы:
module Main where
addEvens :: Int -> Int -> Int
addEvens a b
| even a && even b = a + b
q = zipWith addEvens [0, 2, 4, 6, 7, 8, 10] (repeat 0)
main = print q
Для того, чтобы воспользоваться флагом xc необходимо скомпилировать программу с возможностью профилирования:
$ ghc --make break.hs -rtsopts -prof $ ./break +RTS -xc *** Exception (reporting due to +RTS -xc): (THUNK_2_0), stack trace: Main.CAF break: break.hs:(4,1)-(5,30): Non-exhaustive patterns in function addEvens
Так мы узнали в каком месте кода проявился злосчастный вызов, это строки (4,1)-(5,30). Что соответствует определению функции addEvens. Не очень полезная информация. Мы и так бы это узнали. Нам бы хотелось узнать тот путь, по которому шла программа к этому вызову. Проблема в том, что все вызовы слились в один CAF для модуля. Так разделим их:
$ ghc --make break.hs -rtsopts -prof -caf-all -auto-all $ ./break +RTS -xc *** Exception (reporting due to +RTS -xc): (THUNK_2_0), stack trace: Main.addEvens, called from Main.q, called from Main.CAF:q --> evaluated by: Main.main, called from :Main.CAF:main break: break.hs:(4,1)-(5,30): Non-exhaustive patterns in function addEvens
Теперь мы видим путь к этому вызову, мы пришли в него из значения q, которое было вызвано из main.
В этом разделе мы поговорим о том этапе компиляции, на котором происходят преобразования Core -> Core. Мы называли этот этап упрощением программы.
Мы можем задавать степень оптимизации программы специальными флагами. Самые простые флаги начинаются с большой буквы O. Естественно, чем больше мы оптимизируем, тем дольше компилируется код. Поэтому не стоит увлекаться оптимизацией на начальном этапе проектирования. Посмотрим какие возможности у нас есть:
-O – минимум оптимизаций, код компилируется как можно быстрее.-O0 – выключить оптимизацию полностью-O – умеренная оптимизация.O2 – активная оптимизация, код компилируется дольше, но пока O2 не сильно выигрывает у O по продуктивности.Для оптимизации мы компилируем программу с заданным флагом, например попробуйте скомпилировать самый первый пример с флагом O:
ghc --make sum.hs -O
и утечка памяти исчезнет.
Посмотреть описание конкретных шагов оптимизации можно в документации к GHC. Например при включённой оптимизации GHC применяет анализ строгости. В ходе него GHC может исправить простые утечки памяти за нас. Стоит отметить оптимизацию -fexcess-precision, он может существенно ускорить программы, в которых много вычислений с Double. Но при этом вычисления могут потерять в точности, округление становится непредсказуемым.
Если мы посмотрим в исходный файл для модуля Prelude, то мы найдём такое определение для композиции функций:
-- | Function composition.
{-# INLINE (.) #-}
-- Make sure it has TWO args only on the left, so that it inlines
-- when applied to two functions, even if there is no final argument
(.) :: (b -> c) -> (a -> b) -> a -> c
(.) f g = \x -> f (g x)
Помимо знакомого нам определения и комментариев мы видим новую прагму INLINE. Она указывает компилятору на то, что на этапе упрощения программы необходимо заменить вызов функции на её правую часть. Этот процесс называют встраиванием функций. Замена будет произведена только в случае полного применения функции, если синтаксическая арность (количество аргументов слева от знака равно) совпадает с числом переданных в функцию аргументов. Поэтому для GHC есть существенная разница между определениями:
(.) f g = \x -> f (g x) (.) f g x = f (g x)
Встраиванием функций мы экономим на создании лишних объектов в куче, но при этом код может существенно разбухнуть. GHC пользуется эвристическим алгоритмом при определении когда функцию стоит встраивать, а когда – нет. По умолчанию GHC проводит встраивание только внутри модуля. Если мы компилируем с флагом O, функции будут встраиваться между модулями. Для этого GHC сохраняет в интерфейсном файле (с расширением .hi) не только типы функций, но и правые части достаточно кратких функций. Длина функции определяется числом узлов в синтаксическом дереве кода её правой части. Директивой INLINE мы приказываем GHC встроить функцию. Также есть более слабая версия этой прагмы –INELINABLE. Этой прагмой мы рекомендуем произвести встраивание функции не смотря на её величину.
Задать порог величины функции для встраивания можно с помощью флага -funfolding-use-threshold=16. Отметим, что если функция не является экспортируемой и используется лишь один раз, то GHC встроит её в любом случае, поэтому стоит определять списки экспортируемых определений в шапке модуля, иначе компилятор будет считать, что экспортируются все определения.
Прагма INLINE может стоять в любом месте, где можно было бы объявить тип значения. Так например можно указать компилятору встраивать методы класса:
instance Monad T where
{-# INLINE return #-}
return = ...
{-# INLINE (>>=) #-}
(>>=) = ...
Встраивание значений может существенно ускорить программу. Но не стоит венчать каждую экспортируемую функцию прагмой INLINE, возможно GHC встроит их автоматически. Посмотреть какие функции были встроены можно по определениям, попавшим в файл .hi.
Например если мы скомпилируем такой код с флагом ddump-hi:
module Inline(f, g) where g :: Int -> Int g x = x + 2 f :: Int -> Int f x = g $ g x
то среди прочих определений увидим:
ghc -c -ddump-hi -O Inline.hs
...
f :: GHC.Types.Int -> GHC.Types.Int
{- Arity: 1, HasNoCafRefs, Strictness: U(L)m,
Unfolding: InlineRule (1, True, False)
(\ x :: GHC.Types.Int ->
case x of wild { GHC.Types.I# x1 ->
GHC.Types.I# (GHC.Prim.+# (GHC.Prim.+# x1 2) 2) }) -}
...
В этом виде прочесть функцию не так просто. Ко всем именам добавлены имена модулей. Приведём вывод к более простому виду с помощью флага dsuppress-all:
ghc -c -ddump-hi -dsuppress-all -O Inline.hs
...
f :: Int -> Int
{- Arity: 1, HasNoCafRefs, Strictness: U(L)m,
Unfolding: InlineRule (1, True, False)
(\ x :: Int -> case x of wild { I# x1 -> I# (+# (+# x1 2) 2) }) -}
...
Мы видим, что все вызовы функции g были заменены. Если вы всё же подозреваете, что GHC не справляется с встраиванием ваших часто используемых функций и это сказывается, попробуйте добавить к ним INLINE, но при этом лучше узнать, привело ли это к росту производительности, проверить с помощью профилирования.
Отметим также прагму NOINLINE с её помощью мы можем запретить встраивание функции. Эта прагма часто используется при различных трюках с unsafePerformIO, встраивание функции, которая содержит неконтролируемые побочные эффекты, может повлиять на её результат.
Разработчики GHC хотели, чтобы их компилятор был расширяемым и программист мог бы определять специфические для его приложения правила оптимизации. Для этого была придумана прагма RULES. За счёт чистоты функций мы можем в очень простом виде выражать инварианты программы. Инвариант – это некоторое свойство значения, которое остаётся постоянным при некоторых преобразованиях. Наиболее распространённые инварианты имеют собственные имена. Например, это коммутативность сложения:
forall a b. a + b = b + a
Здесь мы пишем: для любых a и b изменение порядка следования аргументов у (+) не влияет на результат. С ключевым словом forall мы уже когда-то встречались, когда говорили о типе ST. Помните тип функции runST? Пример свойства функции map:
forall f g. map f . map g = map (f . g)
Это свойство принято называть дистрибутивностью. Мы видим, что функция композиции дистрибутивна относительно функции map. Инварианты определяют скрытые закономерности значений. За счёт чистоты функций мы можем безболезненно заменить в любом месте программы левую часть на правую или наоборот. Оптимизация начинается тогда, когда мы понимаем, что одна из частей может быть вычислена гораздо эффективнее другой. Так в примере с map выражение справа от знака равно гораздо эффективнее, поскольку в нём мы не строим промежуточный список. Особенно ярко разница проявляется в энергичной стратегии вычислений. Или посмотрим на такое совсем простое свойство:
map id = id
Если мы заменим левую часть на правую, то число сэкономленных усилий будет пропорционально длине списка. Вряд ли программист станет писать такие выражения, однако они могут появиться после выполнения других оптимизаций, например после многих встраиваний различных функций.
Можно представить, что эти правила являются дополнительными уравнениями в определении функции:
map f [] = [] map f (x:xs) = f x : map f xs map id a = a map f (map g x) = map (f . g) x
Словно теперь мы можем проводить сопоставление с образцом не только по конструкторам, но и по выражениям самого языка и функция map стала конструктором. Что интересно, зависимости могут быть какими угодно, они могут выражать закономерности, присущие той области, которую мы описываем. В дополнительных уравнениях мы подставляем аргументы так же как и в обычных, если где-нибудь в коде программы находится соответствие с левой частью уравнения, мы заменяем её на правую. При этом мы пишем правила так, чтобы действительно происходила оптимизация программы, поэтому слева пишется медленная версия.
Такие дополнительные правила пишутся в специальной прагме RULES:
{-# RULES
"map/compose" forall f g x. map f (map g x) = map (f . g) x
"map/id" map id = id
#-}
Первым в кавычках идёт имя правила. Оно используется только для подсчёта статистики (например если мы хотим узнать сколько правил сработало в данном прогоне программы). За именем правила пишут уравнение. В одной прагме может быть несколько уравнений. Правила разделяются точкой с запятой или переходом на другу строку. Все свободные переменные правила перечисляются в окружении forall (...) .~. Компилятор доверяет нам абсолютно. Производится только проверка типов. Никаких других проверок не проводится. Выполняется ли на самом деле это свойство, будет ли вычисление правой части действительно проще программы вычисления левой – известно только нам.
Отметим то, что прагма RULES применяется до тех пор пока есть возможность её применять, при этом мы можем войти в бесконечный цикл:
{-# RULES
"infinite" forall a b. f a b = f b a
#-}
С помощью прагмы RULES можно реализовать очень сложные схемы оптимизации. Так в Prelude реализуется слияние (fusion) списков. За счёт этой оптимизации многие выражения вида свёртка/развёртка не будут производить промежуточных списков. Этой схеме будет посвящена отдельная глава. Например если список преобразуется серией функций map, filter и foldr промежуточные списки не строятся.
Посмотрим как работает прагма RULES, попробуем скомпилировать такой код:
module Main where
data List a = Nil | Cons a (List a)
deriving (Show)
foldrL :: (a -> b -> b) -> b -> List a -> b
foldrL cons nil x = case x of
Nil -> nil
Cons a as -> cons a (foldrL cons nil as)
mapL :: (a -> b) -> List a -> List b
mapL = undefined
{-# RULES
"mapL" forall f xs.
mapL f xs = foldrL (Cons . f) Nil xs
#-}
main = print $ mapL (+100) $ Cons 1 $ Cons 2 $ Cons 3 Nil
Функция mapL не определена, вместо этого мы сделали косвенное определение в прагме RULES. Проверим, для того чтобы RULES заработали, необходимо компилировать с одним из флагов оптимизаций O или O2:
$ ghc --make -O Rules.hs $ ./Rules Rules: Prelude.undefined
Что-то не так. Дело в том, что GHC проводит встраивание простых функций. GHC слишком поторопился и заменил mapL на её определение. Также обратим внимание на то, что выражение не соответствует левой части правила. У нас:
mapL f xs =/= mapL f $ xs
Функция $ также является простой и GHC встраивает её. Для успешной замены нам необходимо, чтобы $ встроился раньше mapL и чтобы наше правило сработало раньше встраивания mapL.
Для решения этой проблемы в прагмы RULES и INLINE были введены ссылки на фазы компиляции. С помощью них мы можем указать GHC в каком порядке реагировать на эти прагмы. Фазы пишутся в квадратных скобках:
{-# INLINE [2] someFun #-}
{-# RULES
"fun" [0] forall ...
"fun" [1] forall ...
"fun" [~1] forall ...
#-}
Компиляция выполняется в несколько фаз. Фазы следуют от некоторого заданного целого числа, например трёх, до нуля. Мы можем сослаться на фазу двумя способами: просто номером и номером с тильдой. Ссылка без тильды говорит: не применяй правило до наступления данной фазы, далее – применяй. Ссылка c тильдой говорит: попытайся применить это правило как можно раньше – до наступления данной фазы, далее – не применяй.
В нашем примере мы задержим встраивание для mapL и foldrL так:
{-# INLINE [1] foldrL #-}
foldrL :: (a -> b -> b) -> b -> List a -> b
{-# INLINE [1] mapL #-}
mapL :: (a -> b) -> List a -> List b
Посмотреть какие правила сработали можно с помощью флага ddump-rule-firings. Теперь скомпилируем:
$ ghc --make -O Rules.hs -ddump-rule-firings ... Rule fired: SPEC Main.$fShowList [GHC.Integer.Type.Integer] Rule fired: mapL Rule fired: Class op show ... $ ./Rules Cons 101 (Cons 102 (Cons 103 Nil))
Среди прочих правил, определённых в стандартных библиотеках, сработало и наше.
Наш основной враг на этапе оптимизации программы это лишние объекты кучи. Чем меньше объектов мы создаём на пути к результату, тем эффективнее наша программа. С помощью прагмы INLINE мы можем избавиться от многих объектов, связанных с вызовом функции, это объекты типа FUN. Прагма UNPACK позволяет нам бороться с лишними объектами типа CON. В прошлой главе мы говорили о том, что значения в Haskell содержат дополнительную служебную информацию, которая необходима на этапе вычисления, например значение сначала было отложенным, потом мы до него добрались и вычислили, возможно оно оказалось не определённым значением (undefined). Такие значения называются запакованными (boxed). Незапакованное значение, это примитивное значение, как оно представлено в памяти компьютера. Вспомним определение целых чисел:
data Int = I# Int#
По традиции все незапакованные значения пишутся с решёткой на конце. Запакованные значения позволяют откладывать вычисления, пользоваться undefined при определении функции. Но за эту гибкость приходится платить. Вспомним расход памяти в выражении [Pair 1 2]
nil = [] -- глобальный объект (не в счёт)
let x1 = I# 1 -- 2 слова
x2 = I# 2 -- 2 слова
p = Pair x1 x2 -- 3 слова
val = Cons p nil -- 3 слова
in val ------------
-- 10 слов
Получилось десять слов для списка из одного элемента, который фактически хранит два значения. Размер списка, который хранит такие пары будет зависеть от числа элементов $N$ как $10N$. Тогда как полезная нагрузка составляет $2N$. С помощью прагмы UNPACK мы можем отказаться от ленивой гибкости в пользу меньшего расхода памяти. Эта прагма позволяет встраивать
один конструктор в поле другого. Это поле должно быть строгим (с пометкой !) и мономорфным (тип поля должен быть конкретным типом, а не параметром), причём подчинённый тип должен содержать лишь один конструктор (у него нет альтернатив):
data PairInt = PairInt
{-# UNPACK #-} !Int
{-# UNPACK #-} !Int
Мы конкретизировали поля Pair и сделали их строгими с помощью восклицательных знаков. После этого значения из конструктора Int будут храниться прямо в конструкторе PairInt:
nil = [] -- глобальный объект (не в счёт)
let p = PairInt 1 2 -- 3 слова
val = Cons p nil -- 3 слова
in val ------------
-- 6 слов
Так мы сократим размер до $6N$. Но мы можем пойти ещё дальше. Если этот тип является ключевым типом нашей программы и мы рассчитываем на то, что в нём будет хранится много значений мы можем создать специальный список для таких пар и распаковать значение списка:
data ListInt = ConsInt {-# UNPACK #-} !PairInt
| NilInt
nil = NilInt
let val = ConsInt 1 2 nil -- 4 слова
in val -----------
-- 4 слова
Значение будет встроено дважды и получится, что у нашего нового конструктора Cons уже три поля. Отметим, что эта прагма имеет смысл лишь при включённом флаге оптимизации -O или выше. Если мы не включим этот флаг, то компилятор не будет проводить встраивание функций, поэтому при вычислении функций вроде
sumPair :: PairInt -> Int sumPair (Pair a b) = a + b
Плюс не будет встроен и вместо того, чтобы сразу сложить два числа с помощью примитивной функции, компилятор сначала запакует их в конструктор I# и затем применит функцию +, в которой опять распакует их, сложит и затем, снова запаковав, вернёт результат.
Компилятор автоматически запаковывает все такие значения при передаче в ленивую функцию, это может привести к снижению быстродействия даже при включённом флаге оптимизации, при недостаточном встраивании. Это необходимо учитывать. В таких случая проводите профилирование, убедитесь в том, что оптимизация привела к повышению эффективности.
В стандартных библиотеках предусмотрено много незапакованных типов. Например это специальные кортежи. Они пишутся с решётками:
newtype ST s a = ST (STRep s a) type STRep s a = State# s -> (# State# s, a #)
Это определение типа ST. Специальные кортежи используются для возврата нескольких значений напрямую, без создания промежуточного кортежа в куче. В этом случае значения будут сохранены в регистрах или на стеке. Для использования специальных значений необходимо активировать расширения MagicHash и UnboxedTuples
Разработчики различных библиотек могут предоставлять несколько вариантов своих данных: ленивые версии и незапакованные. Например в ST-массив незапакованных значений STUArray s i a эквивалентен массиву значений в C. В таком массиве можно хранить лишь примитивные типы.
Эта глава была посвящена компилятору GHC. Мы говорим Haskell подразумеваем GHC, говорим GHC подразумеваем Haskell. К сожалению на данный момент у этого компилятора нет достойных конкурентов. А может и к счастью, ведь если бы не было GHC, у нас была бы бурная конкуренция среди компиляторов поплоше. Мы бы не знали, что они не так хороши. Но у нас не было бы программ, которые способны тягаться по скорости с С. И мы бы говорили: ну декларативное программирование, что поделаешь, за радость абстракций приходится платить. Но есть GHC! Всё-таки это очень трудно: написать компилятор для ленивого языка
Отметим другие компиляторы: Hugs разработан Марком Джонсом (написан на C), nhc98 основанный Николасом Райомо (Niklas Röjemo) этот компилятор задумывался как легковесный и простой в установке, он разрабатывался при поддержке NUTEK, Йоркского университета и Технического университета Чалмерса. От этого компилятора отпочковался YHC, Йоркский компилятор. UHC – компилятор Утрехтского университета, разработан для тестирования интересных идей в теории типов. JHC (Джон Мичэм, John Meacham) и LHC (Дэвид Химмельступ и Остин Сипп, David Himmelstrup, Austin Seipp) компиляторы предназначенные для проведения более сложных оптимизаций программ с помощью преобразований дерева программы.
В этой главе мы узнали как вычисляются программы в GHC. Мы узнали об этапах компиляции. Сначала проводится синтаксический анализ программы и проверка типов, затем код Haskell переводится на язык Core. Это сильно урезанная версия Haskell. После этого проводятся оптимизации, которые преобразуют дерево программы. На последнем этапе Core переводится на ещё более низкоуровневый, но всё ещё функциональный язык STG, который превращается в низкоуровневый код и исполняется вычислителем. Посмотреть на текст вашей программы в Core и STG можно с помощью флагов ddump-simpl ddump-stg при этом лучше воспользоваться флагом ddump-suppress-all для пропуска многочисленных деталей. Хардкорные разработчики Haskell смотрят Core для того чтобы понять насколько строгой оказалась та или иная функция, как аргументы размещаются в памяти. Но это уже высший пилотаж искусства оптимизации на Haskell.
Мы узнали о том как работает сборщик мусора и научились просматривать разные параметры работы программы. У нас появилось несколько критериев оценки производительности программ: минимум глубоких очисток и отсутствие горбов на графике изменения кучи. Мы потренировались в охоте за утечками памяти и посмотрели как разные типы профилирования могут подсказать нам в каком месте затаилась ошибка. Отметим, что не стоит в каждой медленной программе искать утечку памяти. Так в примере concat у нас не было утечек памяти, просто один из алгоритмов работал очень плохо и через профилирование функций мы узнали какой.
Также мы познакомились с новыми прагмами оптимизации программ. Это встраиваемые функции INLINE, правила преобразования выражений RULE и встраиваемые конструкторы UNPACK. Разработчики GHC отмечают, что грамотное использование прагмы INLINE может существенно повысить скорость программы. Если мы встраиваем функцию, которая используется очень часто, нам не нужно создавать лишних отложенных вычислений при её вызовах.
Надеюсь, что содержание этой главы упростит понимание программ. Как они вычисляются, куда идёт память, почему она висит в куче. При оптимизации программ предпочитайте изменение алгоритма перед настройкой параметров компилятора под плохой алгоритм. Вспомните самый первый пример, увеличением памяти под сборку мусора нам удалось вытянуть ленивую версию sum, но ведь строгая версия требовала в 100 раз меньше памяти, причём её запросы не зависели от величины списка. Если бы мы остановились на ленивой версии, вполне могло бы так статься, что первый год нас бы устраивали результаты, но потом наши аппетиты могли возрасти. И вдруг программа, так тщательно настроенная, взорвалась. За год мы, конечно, многое позабыли о её внутренностях, искать ошибку было бы гораздо труднее. Впрочем не так безнадёжно: включаем auto-all, caf-all с флагом prof и смотрим отчёт после флага p.
Попытайтесь понять причину утечки памяти в примере с функцией sum2 на уровне STG. Не запоминайте этот пример, вроде, ага, тут у нас копятся отложенные вычисления в аргументе. Переведите на STG и посмотрите в каком месте происходит слишком много вызовов let-выражений. Переведите и пример без утечки памяти, а также промежуточный вариант, который не сработал. Для этого вам понадобится выразить энергичный образец через функцию seq.
Подсказка: За счёт семантики case-выражений нам не нужно специальных конструкций для того чтобы реализовать seq в STG:
seq = FUN( a b ->
case a of
x -> b
)
При этом вызов функции seq будет встроен. Необходимо будет заменить в коде все вызовы seq на правую часть определения (без FUN). Также обратите внимание на то, что плюс не является примитивной функцией:
plusInt = FUN( ma mb ->
case ma of
I# a -> case mb of
I# b -> case (primitivePlus a b) of
res -> I# res
)
В этой функции всплыла на поверхность одна тонкость. Если бы мы писали это выражение в Haskell, то мы бы сразу вернули результат (I# (primitivePlus a b)), но мы пишем в STG и конструктор может принять только атомарное выражение. Тогда мы могли бы подумать и сохранить его по старинке в let-выражении:
-> let v = primitivePlus a b in I# v
Но это не правильное выражение в STG! Конструкция в правой части let-выражения должна быть объектом кучи, а у нас там простое выражение. Но было бы плохо добавить к нему THUNK, поскольку это выражение содержит вызов примитивной функции на незапакованных значениях. Эта операция выполняется очень быстро. Было бы плохо создавать для неё специальный объект на куче. Поэтому мы сразу вычисляем это выражение в третьем case. Эта функция также будет встроенной, необходимо заменить все вызовы на определение.
Набейте руку в профилировании, пусть это станет привычкой. Вы долго писали большую программу и теперь вы можете узнать много подробностей из её жизни, что происходит с ней во время вычисления кода. Вернитесь к прошлой главе и попрофилируйте разные примеры. В конце главы мы рассматривали пример с поиском корней, там мы создавали большой список промежуточных результатов и в нём искали решение. Я говорил, что такие алгоритмы очень эффективны при ленивой стратегии вычислений, но так ли это? Будьте критичны, не верьте на слово, ведь теперь у вас есть инструменты для проверки моих туманных гипотез.
Откройте документацию к GHC. Пролистайте её. Проникнитесь уважением к разработчикам GHC. Найдите исходники GHC и почитайте их. Посмотрите на Haskell-код, написанный профессионалами. Выберите функцию наугад и попытайтесь понять как она строит свой результат.
Откройте документацию вновь. Нас интересует глава Profiling. Найдите в разделе профилирование кучи как выполняется retainer profiling. Это специальный тип профилирования направленный на поиск данных, которые удерживают в памяти другие данные (типичный сценарий для утечек памяти). Разберитесь с этим типом профилирования (флаг hr).
Постройте систему правил, которая выполняет слияние для списков List, определённых в примере для прагмы RULES. Сравните показатели производительности с правилами и без (для этого скомпилируйте дважды с флагом O и без) на тестовом выражении:
main = print $ sumL $
mapL (\x -> x - 1000) $ mapL (+100) $ mapL (*2) $ genL 0 1e6
Функция sumL находит сумму элементов в списке, функция genL генерирует список чисел с единичным шагом от первого аргумента до второго.
Подсказка: вам нужно воспользоваться такими свойствами (не забудьте о фазах компиляции)
mapL f (mapL g xs) = ... foldrL cons nil (mapL f xs) = ...
Откройте исходный код Prelude и присмотритесь к различным прагмам. Попытайтесь понять почему они там используются.