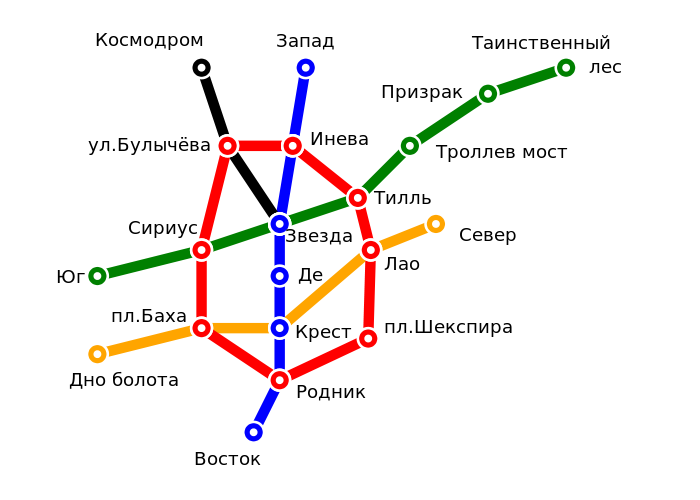
Схема метрополитена
Рассмотрим задачу поиска маршрута на карте. У нас есть карта метро и нам нужно проложить маршрут от одной станции к другой. Карта метро~– это граф, узлы обозначают станции, а рёбра соединяют соседние станции. Предположим, что мы знаем расстояния между всеми станциями и нам надо найти кратчайший путь от станции площадь Баха до станции Таинственный лес.

Схема метрополитена
Давайте переведём этот рисунок на Haskell. Сначала опишем имена линий и станций:
module Metro where
data Station = St Way Name
deriving (Show, Eq)
data Way = Blue | Black | Green | Red | Orange
deriving (Show, Eq)
data Name = Kosmodrom | UlBylichova | Zvezda
| Zapad | Ineva | De | Krest | Rodnik | Vostok
| Yug | Sirius | Til | TrollevMost | Prizrak | TainstvenniyLes
| DnoBolota | PlBakha | Lao | Sever
| PlShekspira
deriving (Show, Eq)
Предположим, что нам известны координаты каждой из станций. По ним мы можем вычислять расстояние между станциями по прямой:
data Point = Point
{ px :: Double
, py :: Double
} deriving (Show, Eq)
place :: Name -> Point
place x = uncurry Point $ case x of
Kosmodrom -> (-3,7)
UlBylichova -> (-2,4)
Zvezda -> (0,1)
Zapad -> (1,7)
Ineva -> (0.5, 4)
De -> (0,-1)
Krest -> (0,-3)
Rodnik -> (0,-5)
Vostok -> (-1,-7)
Yug -> (-7,-1)
Sirius -> (-3,0)
Til -> (3,2)
TrollevMost -> (5,4)
Prizrak -> (8,6)
TainstvenniyLes -> (11,7)
DnoBolota -> (-7,-4)
PlBakha -> (-3,-3)
Lao -> (3.5,0)
Sever -> (6,1)
PlShekspira -> (3,-3)
dist :: Point -> Point -> Double
dist a b = sqrt $ (px a - px b)^2 + (py a - py b)^2
stationDist :: Station -> Station -> Double
stationDist (St n a) (St m b)
| n /= m && a == b = penalty
| otherwise = dist (place a) (place b)
where penalty = 1
Расстояние между точками вычисляется по формуле Евклида (dist). Если у станций одинаковые имена, но они расположены на разных линиях мы будем считать, что расстояние между ними равно единице. Теперь нам необходимо описать связность станций. Мы опишем связность в виде функции, которая для данной станции возвращает список всех соседних с ней станций:
metroMap :: Station -> [Station]
metroMap x = case x of
St Black Kosmodrom -> [St Black UlBylichova]
St Black UlBylichova ->
[St Black Kosmodrom, St Black Zvezda, St Red UlBylichova]
St Black Zvezda ->
[St Black UlBylichova, St Blue Zvezda, St Green Zvezda]
...
Приведён пример заполнения только для одной линии. Остальные линии заполняются аналогично. Обратите внимание на то, что некоторые станции имеют одинаковые имена, но находятся на разных линиях.
Всё готово для того чтобы написать функцию поиска маршрута. Для этого мы воспользуемся алгоритмом A*.
Наша задача относится к задачам поиска путей на графе. Путём на графе называют такую последовательность узлов, в которой для любых двух соседних узлов существует ребро, которое их соединяет. В нашем случае графом является карта метро, узлами~– станции, рёбрами~– линии между станциями, а путями~– маршруты.
Представим, что мы находимся в узле A и нам необходимо попасть в узел B и единственное, что нам известно~– это все соседние узлы с тем, в котором мы находимся. У нас есть возможность перейти в один из соседних узлов и посмотреть нет ли среди их соседей узла B. В этом случае нам ничего не остаётся кроме того как бродить по карте от станции к станции в случайном порядке, пока мы не натолкнёмся на узел B или все узлы не кончатся. Такой поиск называют слепым.
Вот если бы у нас был компас, который в каждой точке указывал в сторону цели нам было бы гораздо проще. Такой компас принято называть эвристикой. Это функция, которая принимает узел и возвращает число. Чем меньше число, тем ближе узел к цели. Обычно эвристика указывает не точное расстояние до цели, поскольку мы не знаем где цель, а приблизительную оценку. Мы не знаем расстояние до цели, но догадываемся, нам кажется, что она где-то там, ещё чуть-чуть и мы найдём её. Примером эвристики для поиска по карте может быть функция, которая вычисляет расстояние по прямой до цели. Предположим, что мы не знаем где находится цель (какая дорога к ней ведёт), но мы знаем её координаты. Также мы знаем координаты каждой вершины, в которой мы находимся. Тогда мы можем легко вычислить расстояние по прямой до цели и наш поиск станет гораздо более осмысленным.
Так находясь в точке A мы можем сразу пойти в тот соседний узел, который ближе всех к цели. Такой поиск называют поиском по первому лучшему приближению. В поиске A* учитывается не только расстояние до цели, но и то расстояние, которое мы уже прошли. Мы выбираем не ту вершину, которая ближе к цели, а ту для которой полный путь до цели будет минимальным. Ведь пока мы идём мы можем запоминать какое расстояние мы уже прошли. Прибавив к этому значению, то которое мы получим с помощью эвристики мы получим полный (предполагаемый) путь до цели.
Поиск А* гораздо лучше поиска по первому лучшему приближению. Его часто применяют в компьютерных играх для поиска пути или принятия решений.
Принято разделять поиск на графе и поиск на дереве. Если мы идём по графу, то вершины могут повторятся (они образуют циклы). В случае поиска на дереве мы считаем, что все вершины уникальны. При поиске на графе очень важно запоминать те вершины, в которых мы уже побывали. Иначе мы будем очень часто ходить кругами.
В Haskell очень удобно работать с данными, которые имеют иерархическую структуру. Их можно представить в виде дерева, обычно в таких типах у нас есть конструкторы-константы и конструкторы, которые собирают составные значения. Граф выходит за рамки этого класса данных, потому что рёбра графов могут образовывать циклы. Но мы схитрим и представим граф поиска в виде дерева. Корнем нашего дерева будет начальная точка поиска, а поддеревьями для данной вершины узла будут все вершины-соседи. В таком дереве будет очень много повторяющихся узлов, так например мы можем пойти в соседнюю вершину, потом вернуться обратно, опять пойти в туже соседнюю вершину, и так до бесконечности. Для того, чтобы избежать подобных ситуаций мы будем запоминать те вершины, в которых мы уже побывали и не рассматривать их, если они встретятся нам ещё раз.
Сформулируем задачу поиска в типах. У нас есть дерево поиска, которое содержит все возможные разветвления, также каждая вершина содержит значение эвристики, по нему мы знаем насколько близка данная вершина к цели. Также у нас есть специальный предикат, который определён на вершинах, по нему мы можем узнать является ли данная вершина целью. Нам нужно получить путь, или цепочку вершин, которая будет начинаться в корне дерева поиска и заканчиваться в целевой вершине.
search :: Ord h => (a -> Bool) -> Tree (a, h) -> Maybe [a]
Здесь a – это значение вершины и h – значение эвристики. Обратите внимание на зависимость Ord h в контексте, ведь мы собираемся сравнивать эти значения по близости к цели. При обходе дерева мы будем запоминать повторяющиеся вершины, для этого мы воспользуемся типом множество из стандартного модуля Data.Set. Внутри Set могут хранится только значения, для которых определены операции сравнения, поэтому нам придётся добавить в контекст ещё одну зависимость:
import Data.Tree import qualified Data.Set as S search :: (Ord h, Ord a) => (a -> Bool) -> Tree (a, h) -> Maybe [a]
Поиск будет заключаться в том, что мы будем обходить дерево от корня к узлам. При этом среди всех узлов-альтернатив мы будем просматривать узлы с наименьшим значением эвристики. В этом нам поможет специальная структура данных, которая называется очередью с приоритетом (priority queue). Эта очередь хранит элементы с учётом их старшинства (приоритета). Мы можем добавлять в неё элементы и извлекать элементы. При этом мы всегда будем извлекать элемент с наименьшим приоритетом. Мы воспользуемся очередями из библиотеки fingertree. Для начала установим библиотеку:
cabal install fingertree
Теперь посмотрим в документацию и узнаем какие функции нам доступны. Документацию к пакету можно найти на сайте http://hackage.haskell.org/package/fingertree. Пока отложим детальное изучение интерфейса, отметим лишь то, что мы можем добавлять элементы к очереди и извлекать элементы с учётом приоритета:
insert :: Ord k => k -> v -> PQueue k v -> PQueue k v minView :: Ord k => PQueue k v -> Maybe (v, PQueue k v)
Вернёмся к функции search. Я бы хотел обратить ваше внимание на то, как мы будем разрабатывать эту функцию. Вспомним, что Haskell – ленивый язык. Это означает, что при обработке рекурсивных типов данных, функция “углубляется” в значение лишь тогда, когда функция, которая вызвала эту функцию попросит её об этом. Это даёт нам возможность работать с потенциально бесконечными структурами данных и, что более важно, разделять сложный алгоритм на независимые составляющие.
В функции search нам необходимо обойти все элементы в порядке значения эвристики и остановиться в вершине, на которой целевой предикат вернёт True. Но для начала мы добавим к вершинам их пути из корня, для того чтобы в конце мы смогли узнать как мы попали в текущую вершину. Итак наша функция разбивается на три составляющие:
search :: (Ord h, Ord a) => (a -> Bool) -> Tree (a, h) -> Maybe [a] search isGoal = findPath isGoal . flattenTree . addPath
выпишем типы составляющих функций и проверим код в интерпретаторе.
un = undefined
findPath :: (a -> Bool) -> [Path a] -> Maybe [a]
findPath = un
flattenTree :: (Ord h, Ord a) => Tree (Path a, h) -> [Path a]
flattenTree = un
addPath :: Tree (a, h) -> Tree (Path a, h)
addPath = un
data Path a = Path
{ pathEnd :: a
, path :: [a]
}
Обратите внимание на то как поступающие на вход данные разделились между функциями. Информация о приоритете вершин не идёт дальше функции flattenTree, а предикат isGoal используется только в функции findPath. Модуль прошёл проверку типов и мы можем детализировать функции дальше:
addPath :: Tree (a, h) -> Tree (Path a, h)
addPath = iter []
where iter ps t = Node (Path val (reverse ps'), h) $
iter ps' <$> subForest t
where (val, h) = rootLabel t
ps' = val : ps
В этой функции мы просто присоединяем к данной вершине все родительские вершины, так мы составляем маршрут от данной вершины до начальной, поскольку мы всё время добавляем новые вершины в начало списка, в итоге у нас получаются перевёрнутые маршруты, поэтому перед тем как обернуть значение в конструктор Path мы переворачиваем список. На самом деле нам нужно перевернуть только один путь. Путь, который ведёт к цели, но за счёт того, что язык у нас ленивый, функция reverse будет применена не сразу, а лишь тогда, когда нам действительно понадобится значение пути. Это как раз и произойдёт лишь один раз, в самом конце программы, лишь для одного значения!
Давайте пока пропустим функцию flattenTree и сначала определим функцию findPath. Эта функция принимает все вершины, которые мы обошли если бы шли без цели (функции isGoal) и ищет среди них первую, которая удовлетворяет предикату. Для этого мы воспользуемся стандартной функцией find из модуля Data.List:
findPath :: (a -> Bool) -> [Path a] -> Maybe [a] findPath isGoal = fmap path . find (isGoal . pathEnd)
Напомню тип функции find, она принимает предикат и список, а возвращает первое значение списка, на котором предикат вернёт True:
find :: (a -> Bool) -> [a] -> Maybe a
Функция fmap применяется из-за того, что результат функции find завёрнут в Maybe, это частично определённая функция. В самом деле ведь в списке может и не оказаться подходящего значения.
Осталось определить функцию flattenTree. Было бы хорошо определить её так, чтобы она была развёрткой для списка. Поскольку функция find является свёрткой (может быть определена через fold), вместе эти функции работали бы очень эффективно. Мы определим функцию flattenTree через взаимную рекурсию. Две функции будут по очереди вызывать друг друга. Одна из них будет извлекать следующее значение из очереди, а другая – проверять не встречалось ли нам уже такое значение, и добавлять новые элементы в очередь.
flattenTree :: (Ord h, Ord a) => Tree (Path a, h) -> [Path a]
flattenTree a = ping none (singleton a)
ping :: (Ord h, Ord a) => Visited a -> ToVisit a h -> [Path a]
ping visited toVisit
| isEmpty toVisit = []
| otherwise = pong visited toVisit' a
where (a, toVisit') = next toVisit
pong :: (Ord h, Ord a)
=> Visited a -> ToVisit a h -> Tree (Path a, h) -> [Path a]
pong visited toVisit a
| inside a visited = ping visited toVisit
| otherwise = getPath a :
ping (insert a visited) (schedule (subForest a) toVisit)
Типы Visited и ToVisit обозначают наборы вершин, которые мы уже посетили и которые только собираемся посетить. Не вдаваясь в подробности интерфейса этих типов, давайте присмотримся к функциям ping и pong с точки зрения функции, которая их будет вызывать, а именно функции findPath. Эта функция ожидает на входе список. Внутри она обходит список в поисках нужного элемента, поэтому она будет применять сопоставление с образцом, разбирая список на части. Сначала она запросит сопоставление с пустым списком, запустится функция ping с пустым множеством посещённых вершин (none) и одним элементом в очереди вершин (singleton a), которые предстоит посетить. Функция ping проверит не является ли очередь пустой, очередь содержит один элемент, поэтому она перейдёт к следующему случаю и извлечёт из очереди один элемент (next), который будет передан в функцию pong. Функция pong проверит нет ли в списке уже посещённых элементов того, который был только что извлечён (inside a visited). Если это окажется так, то она запросит следующий элемент у функции ping. Если же исходный элемент окажется новым, она добавит его в список (getPath a : ...) и запланирует обход всех дочерних деревьев данного элемента (schedule (subForest a) toVisit). При первом заходе исходный элемент окажется новым и функция findPath поймёт, что список не пустой и остановит вычисление. Она немного передохнёт и примется за следующий случай. Там она будет извлекать первый элемент списка и сопоставлять его с предикатом. При этом первый элемент уже вычислен. Мы воспользуемся этим, убедимся в том, что он не является целью и рекурсивно вызовем функцию find на хвосте списка. Функция findPath запросит следующее значение и так далее.
Наша функция flattenPath не является развёрткой, но очень похожа на неё тем, что позволяет вычислять результирующий список частично. Например функция length требует полного обхода списка. Мы не можем использовать её с бесконечными списками. Теперь давайте разберёмся с подчинёнными функциями:
getPath :: Tree (Path a, h) -> Path a getPath = fst . rootLabel
Функции для множества вершин, которые мы уже посетили:
import qualified Data.Set as S ... type Visited a = S.Set a none :: Ord a => Visited a none = S.empty insert :: Ord a => Tree (Path a, h) -> Visited a -> Visited a insert = S.insert . pathEnd . getPath inside :: Ord a => Tree (Path a, h) -> Visited a -> Bool inside = S.member . pathEnd . getPath
Функции для очереди тех вершин, что мы только собираемся посетить:
import Data.Maybe import qualified Data.PriorityQueue.FingerTree as Q ... type ToVisit a h = Q.PQueue h (Tree (Path a, h)) priority t = (snd $ rootLabel t, t) singleton :: Ord h => Tree (Path a, h) -> ToVisit a h singleton = uncurry Q.singleton . priority next :: Ord h => ToVisit a h -> (Tree (Path a, h), ToVisit a h) next = fromJust . Q.minView isEmpty :: Ord h => ToVisit a h -> Bool isEmpty = Q.null schedule :: Ord h => [Tree (Path a, h)] -> ToVisit a h -> ToVisit a h schedule = Q.union . Q.fromList . fmap priority
Эти функции очень простые, они специализируют более общие функции для типов Set и PQueue, вы наверняка легко разберётесь с ними, заглянув в документацию к модулям Data.Set и Data.PriorityQueue.FingerTree.
Осталось только написать функцию, которая будет составлять дерево поиска для алгоритма A*. Она принимает функцию ветвления, а также функцию расстояния до цели и строит по ним дерево поиска:
astarTree :: (Num h, Ord h)
=> (a -> [(a, h)]) -> (a -> h) -> a -> Tree (a, h)
astarTree alts distToGoal s0 = unfoldTree f (s0, 0)
where f (s, h) = ((s, heur h s), next h <$> alts s)
heur h s = h + distToGoal s
next h (a, d) = (a, d + h)
Теперь давайте посмотрим как наша функция справится с задачей поиска маршрутов в метро:
metroTree :: Station -> Station -> Tree (Station, Double) metroTree init goal = astarTree distMetroMap (stationDist goal) init connect :: Station -> Station -> Maybe [Station] connect a b = search (== b) $ metroTree a b main = print $ connect (St Red Sirius) (St Green Prizrak)
К примеру найдём маршрут от станции “Дно Болота” до станции “Призрак”:
*Metro> connect (St Orange DnoBolota) (St Green Prizrak)
Just [St Orange DnoBolota,St Orange PlBakha,
St Red PlBakha,St Red Sirius,St Green Sirius,
St Green Zvezda,St Green Til,
St Green TrollevMost,St Green Prizrak]
*Metro> connect (St Red PlShekspira) (St Blue De)
Just [St Red PlShekspira,St Red Rodnik,St Blue Rodnik,
St Blue Krest,St Blue De]
*Metro> connect (St Red PlShekspira) (St Orange De)
Nothing
В третьем случае маршрут не был найден, поскольку у нас нет станции De на оранжевой ветке.
Мы проверили три случая, ещё три случая, ещё три случая, ожидаемый результат сходится с тем, что возвращает нам интерпретатор, но можем ли мы быть уверены в том, что алгоритм действительно работает? Для Haskell была разработана специальная библиотека тестирования QuickCheck, которая упрощает процесс проверки программ. Мы можем сформулировать свойства, которые обязательно должны выполняться, а QuickCheck сгенерирует случайный набор данных и проверит наши свойства на них.
Например в нашей задаче путь из A в B должен совпадать с перевёрнутым путём из B в A. Также все станции в маршруте должны быть соседними. Давайте проверим эти свойства. Для этого нам нужно сформулировать их в виде предикатов:
module Test where import Control.Applicative import Metro prop1 :: Station -> Station -> Bool prop1 a b = connect a b == (fmap reverse $ connect b a) prop2 :: Station -> Station -> Bool prop2 a b = maybe True (all (uncurry near) . pairs) $ connect a b pairs :: [a] -> [(a, a)] pairs xs = zip xs (drop 1 xs) near :: Station -> Station -> Bool near a b = a `elem` (fst <$> distMetroMap b)
Установим QuickCheck:
cabal install QuickCheck
Теперь нам нужно подсказать QuickCheck как генерировать случайные значения типа Station. QuickCheck тестирует функции, которые принимают значения из класса Arbitrary и возвращают Bool. Класс Arbitrary отвечает за генерацию случайных значений.
Основной метод arbitrary возвращает генератор случайных значений:
class Arbitrary a where
arbitrary :: Gen a
Мы воспользуемся тем, что этот класс уже определён для многих стандартных типов. Кроме того класс Gen является монадой. Мы сгенерируем случайное целое число и отобразим его в одну из станций. Сделать это можно разными способами, мы начнём из одной станции и будем случайно блуждать по карте:
import Test.QuickCheck
...
instance Arbitrary Station where
arbitrary = ($ s0) . foldr (.) id . fmap select <$> ints
where ints = vector =<< choose (0, 100)
s0 = St Blue De
select :: Int -> Station -> Station
select i s = as !! mod i (length as)
where as = fst <$> distMetroMap s
Мы воспользовались двумя функциями из библиотеки QuickCheck. Это vector и choose. Первая строит список случайных чисел заданной длины, а вторая выбирает случайное число из заданного диапазона. Теперь мы можем протестировать наши предикаты с помощью функции quickCheck:
*Test Prelude> quickCheck prop1 +++ OK, passed 100 tests. *Test Prelude> quickCheck prop2 +++ OK, passed 100 tests. *Test Prelude>
Свойства прошли тестирование на выборке из 100 комбинаций аргументов. Если нам интересно, мы можем с помощью функции verboseCheck посмотреть на каких именно значениях проводилось тестирование:
*Test Prelude> verboseCheck prop2 Passed: St Black Kosmodrom St Red UlBylichova Passed: St Black UlBylichova St Orange Sever Passed: St Red Sirius St Blue Krest ...
Если бы свойство не выполнилось, QuickCheck сообщил бы нам об этом и показал бы те элементы, для которых свойство не выполнилось. Давайте составим такое свойство искусственно. Например, проверим, находятся ли все станции на одной линии:
fakeProp :: Station -> Station -> Bool fakeProp (St a _) (St b _) = a == b
Посмотрим, что на это скажет QuickCheck:
*Test Prelude> quickCheck fakeProp *** Failed! Falsifiable (after 1 test): St Green Sirius St Blue Rodnik
По умолчанию QuickCheck проверит свойство сто раз. Для изменения этих настроек, мы можем воспользоваться функцией quickCheckWith, дополнительным параметром она принимает значение типа Arg, которое содержит параметры тестирования. Например протестируем первое свойство 500 раз:
*Test> quickCheckWith (stdArgs{ maxSuccess = 500 }) prop1
+++ OK, passed 500 tests.
Мы воспользовались стандартными настройками (stdArgs) и изменили один параметр.
Предположим, что мы уверены в правильной работе алгоритма для голубой и чёрной ветки метро, но сомневаемся в остальных. Как раз для этого случая в QuickCheck предусмотрена функция a==>b. Это функция обозначает условную проверку, свойство b будет протестировано только в том случае, если свойство a окажется верным. Иначе тестовые данные будут отброшены.
notBlueAndBlack a b = cond a && cond b ==> prop1 a b
where cond (St a _) = a /= Blue && a /= Black
Далее тестируем как обычно:
*Test> quickCheck notBlueAndBlack +++ OK, passed 100 tests.
Также с помощью функции forAll мы можем подсказать QuickCheck на каких данных тестировать свойство.
forAll :: (Show a, Testable prop) => Gen a -> (a -> prop) -> Property
Эта функция принимает генератор случайных значений и свойство, которое зависит от тех значений, которые создаются этим генератором. К примеру, пусть нас интересуют только все возможные пути между четырьмя станциями: (St Blue De), (St Red Lao), (St Green Til) и (St Orange Sever). Воспользуемся функцией elements :: [a] -> Gen a, она как раз принимает список значений, и возвращает генератор, который случайным образом выбирает любое значение из этого списка.
testFor = forAll (liftA2 (,) gen gen) $ uncurry prop1
where gen = elements [St Blue De, St Red Lao,
St Green Til, St Orange Sever]
Проверим, те ли значения попали в выборку:
*Test> verboseCheckWith (stdArgs{ maxSuccess = 3 }) testFor
Passed:
(St Blue De,St Orange Sever)
Passed:
(St Orange Sever,St Red Lao)
Passed:
(St Red Lao,St Red Lao)
+++ OK, passed 3 tests.
Мы можем настроить формирование выборки ещё одним способом. Для этого мы сделаем специальный тип обёртку над Station и определим для него свой экземпляр класса Arbitrary:
newtype OnlyOrange = OnlyOrange Station
newtype Only4 = Only4 Station
instance Arbitrary OnlyOrange where
arbitrary = OnlyOrange . St Orange <$>
elements [DnoBolota, PlBakha, Krest, Lao, Sever]
instance Arbitrary Only4 where
arbitrary = Only4 <$> elements [St Blue De, St Red Lao,
St Green Til, St Orange Sever]
После этого мы можем очень легко комбинировать различные выборки при тестировании.
*Test> quickCheck $ \(Only4 a) (Only4 b) -> prop1 a b +++ OK, passed 100 tests. *Test> quickCheck $ \(Only4 a) (OnlyOrange b) -> prop1 a b +++ OK, passed 100 tests. *Test> quickCheck $ \a (OnlyOrange b) -> prop2 a b +++ OK, passed 100 tests.
Мы можем попросить у QuickCheck, чтобы он разбил тестовую выборку на классы и в конце тестирования сообщил бы нам сколько элементов в какой класс попали. Это делается с помощью функции classify:
classify :: Testable prop => Bool -> String -> prop -> Property
Она принимает условие классификации, метку класса и свойство. Например так мы можем разбить выборку по типам линий:
prop3 :: Station -> Station -> Property
prop3 a@(St wa _) b@(St wb _) =
classify (wa == Orange || wb == Orange) "Orange" $
classify (wa == Black || wb == Black) "Black" $
classify (wa == Red || wb == Red) "Red" $ prop1 a b
Протестируем:
*Test> quickCheck prop3 +++ OK, passed 100 tests: 34% Red 15% Orange 9% Black 8% Orange, Red 6% Black, Red 5% Orange, Black
Недавно появилась библиотека unordered-containers. Она предлагает более эффективную реализацию нескольких структур из стандартной библиотеки containers. Например там мы можем найти тип HashSet. Почему бы нам не заменить на него стандартный тип Set?
cabal install unordered-containers
Изменения отразятся лишь на контекстах объявлений типов. Элементы, принадлежащие множеству HashSet, должны быть экземплярами классов Eq и Hashable. Новый класс Hashable нужен для ускорения работы с данными. Давайте посмотрим на этот класс:
Prelude> :m Data.Hashable Prelude Data.Hashable> :i Hashable class Hashable a where hash :: a -> Int hashWithSalt :: Int -> a -> Int -- Defined in `Data.Hashable' ... ... много экземпляров
Обязательный метод класса hash даёт нам возможность преобразовать элемент в целое число. Это число называют хеш-ключом. Хеш-ключи используются для хранения элементов в хеш-таблицах. Мы не будем подробно на них останавливаться, отметим лишь то, что они позволяют очень быстро извлекать данные из контейнеров и обновлять данные.
Теперь просто скопируйте модуль Astar.hs измените одну строчку, и добавьте ещё одну (в шапке модуля):
import qualified Data.HashSet as S import Data.Hashable
Попробуйте загрузить модуль в интерпретатор. ghci выдаст длинный список ошибок, это – хорошо. По ним вы сможете легко догадаться в каких местах необходимо заменить Ord a на (Hashable a, Eq a).
Теперь для поиска маршрутов нам необходимо определить экземпляр класса Hashable для типа Station. В модуле Data.Hashable уже определены экземпляры для многих стандартных типов. Мы воспользуемся экземпляром для целых чисел.
Добавим в driving подчинённых типов класс Enum и воспользуемся им в экземпляре для Hashable:
instance Hashable Station where
hash (St a b) = hash (fromEnum a, fromEnum b)
Теперь определим две функции определения маршрута:
import qualified AstarSet as S import qualified AstarHashSet as H ... connectSet :: Station -> Station -> Maybe [Station] connectSet a b = S.search (== b) $ metroTree a b connectHashSet :: Station -> Station -> Maybe [Station] connectHashSet a b = H.search (== b) $ metroTree a b
Как нам сравнить быстродействие двух алгоритмов? Оценка быстродействия программ, написанных на Haskell, может таить в себе подвохи. Например если мы запустим оба алгоритма в одной программе, возможно случится такая ситуация, что часть данных, одинаковая для каждого из методов будет вычислена один раз, а во втором алгоритме переиспользована, и нам может показаться, что второй алгоритм гораздо быстрее первого. Также необходимо учитывать внешние факторы. Тестовая программа вычисляется на одном компьютере, и если алгоритмы тестируются в разное время, может статься так, что мы сидели-сидели и ждали пока тест завершится, в это время работал первый алгоритм, потом нам надоело ждать, мы решили включить музыку, проверить почту, и второму алгоритму досталось меньше вычислительных ресурсов. Все эти факторы необходимо учитывать при тестировании. Как раз для этого и существует замечательная библиотека criterion.
Она проводит серию тестов и по ним оценивает показатели быстродействия. При этом учитывается достоверность тестов. По результатам тестирования показатели сверяются между собой, и если разброс оказывается слишком большим, программа сообщает нам: что-то тут не чисто, данным не стоит доверять. Более того результаты оформляются в наглядные графики, мы можем на глаз оценить распределения и разброс показателей.
Центральным элементом библиотеки является класс Benchmarkable. Он объединяет данные, которые можно тестировать. Среди них чистые функции (тип Pure) и значения с побочными эффектами (тип IO a).
Мы можем превращать данные в тесты (тип Benchmark) с помощью функции bench:
benchSource :: Benchmarkable b => String -> b -> Benchmark
Она добавляет к данным комментарий и превращает их в тесты. Как было отмечено, существует одна тонкость при тестировании чистых функций: чистые функции в Haskell могут разделять данные между собой, поэтому для независимого тестирования мы оборачиваем функции в специальный тип Pure. У нас есть два варианта тестирования:
Мы можем протестировать приведение результата к заголовочной нормальной форме (вспомните главу о ленивых вычислениях):
nf :: NFData b => (a -> b) -> a -> Pure
или к слабой заголовочной нормальной форме:
whnf :: (a -> b) -> a -> Pure
Аналогичные функции (nfIO, whnfIO) есть и для данных с побочными эффектами. Класс NFData обозначает все значения, для которых заголовочная нормальная форма определена. Этот класс пришёл в библиотеку criterion из библиотеки deepseq. Стоит отметить эту библиотеку. В ней определён аналог функции seq. Функция seq приводит значения к слабой заголовочной нормальной форме (мы заглядываем вглубь значения лишь на один конструктор), а функция deepseq проводит полное вычисление значения. Значение приводится к заголовочной нормальной форме.
Также нам пригодится функция группировки тестов:
bgroup :: String -> [Benchmark] -> Benchmark
С её помощью мы объединяем список тестов в один, под некоторым именем. Тестирование проводится с помощью функции defaultMain:
defaultMain :: [Benchmark] -> IO ()
Она принимает список тестов и выполняет их. Выполнение тестов заключается в компиляции программы. После компиляции мы получим исполняемый файл который проводит тестирование в зависимости от параметров, указываемых флагами. До них мы ещё доберёмся, а пока опишем наши тесты:
-- | Module: Speed.hs
module Main where
import Criterion.Main
import Control.DeepSeq
import Metro
instance NFData Station where
rnf (St a b) = rnf (rnf a, rnf b)
instance NFData Way where
instance NFData Name where
pair1 = (St Orange DnoBolota, St Green Prizrak)
pair2 = (St Red Lao, St Blue De)
test name search = bgroup name $ [
bench "1" $ nf (uncurry search) pair1,
bench "2" $ nf (uncurry search) pair2]
main = defaultMain [
test "Set" connectSet,
test "Hash" connectHashSet]
Экземпляр для класса NFData похож на экземпляр для Hashable. Мы также определили метод значения через методы для типов, из которых он состоит. Класс NFData устроен так, что для типов из класса Enum мы можем воспользоваться определением по умолчанию (как в случае для Way и Name).
Теперь перейдём в командную строку, переключимся на директорию с нашим модулем и скомпилируем его:
$ ghc -O --make Speed.hs
Флаг -O говорит ghc, что необходимо провести оптимизацию кода. Появится исполняемый файл Speed. Что мы можем делать с этим файлом? Узнать это можно, запустив его с флагом --help:
Мы можем узнать какие функции нам доступны, набрав:
$ ./Speed --help
I don't know what version I am.
Usage: Speed [OPTIONS] [BENCHMARKS]
-h, -? --help print help, then exit
-G --no-gc do not collect garbage between iterations
-g --gc collect garbage between iterations
-I CI --ci=CI bootstrap confidence interval
-l --list print only a list of benchmark names
-o FILENAME --output=FILENAME report file to write to
-q --quiet print less output
--resamples=N number of bootstrap resamples to perform
-s N --samples=N number of samples to collect
-t FILENAME --template=FILENAME template file to use
-u FILENAME --summary=FILENAME produce a summary CSV file of all results
-V --version display version, then exit
-v --verbose print more output
If no benchmark names are given, all are run
Otherwise, benchmarks are run by prefix match
Из этих настроек самые интересные, это -s и -o. -s указывает число сэмплов выборке (столько раз будет запущен каждый тест). а -o говорит, о том в какой файл поместить результаты. Результаты представлены в виде графиков, формируется файл, который можно открыть в любом браузере. Записать данные в таблицу (например для отчёта) можно с помощью флага -u.
Проверим результаты:
./Speed -o res.html -s 100
Откроем файл res.html и посмотрим на графики. Оказалось, что для данных двух случаев первый алгоритм работал немного лучше. Но выборку из двух вариантов вряд ли можно считать убедительной. Давайте расширим выборку с помощью QuickCheck. Мы запустим проверку какого-нибудь свойства тем и другим методом. В итоге QuickCheck сам сгенерирует достаточное число случайных данных, а criterion оценит быстродействие. Мы проверим самое первое свойство (о перевёрнутых маршрутах) на том и другом алгоритме.
module Main where
import Control.Applicative
import Test.QuickCheck
import Metro
instance Arbitrary Station where
arbitrary = ($ s0) . foldr (.) id . fmap select <$> ints
where ints = vector =<< choose (0, 100)
s0 = St Blue De
select :: Int -> Station -> Station
select i s = as !! mod i (length as)
where as = fst <$> distMetroMap s
prop :: (Station -> Station -> Maybe [Station])
-> Station -> Station -> Bool
prop search a b = search a b == (reverse <$> search b a)
main = defaultMain [
bench "Set" $ quickCheck (prop connectSet),
bench "Hash" $ quickCheck (prop connectHashSet)]
В этом тесте метод Set также оказался совсем немного быстрее.
Как интерпретировать результаты? С левой стороны мы видим оценку плотности вероятности распределения быстродействия. Под графиком мы видим среднее (mean) и дисперсию значения (std dev). Показаны три числа. Это нижняя грань доверительного интервала, оценка величины и верхняя грань доверительного интервала (ci, confidence interval). Среднее значение показывает оценку величины, мы говорим, что алгоритм работает примерно 100 миллисекунд. Дисперсия – это разброс результатов вокруг среднего значения. С правой стороны мы видим графики с точками. Каждая точка обозначает отдельный запуск алгоритма. Количество запусков соответствует флагу -s. В последней строке под графиком criterion сообщает степень недоверия к результатам. В последнем опыте этот показатель достаточно высок. Возможно это связано с тем, что наш алгоритм выбора случайных станций имеет сильный разброс по времени. Ведь сначала мы генерируем случайное число n от 0 до 100, и затем начинаем блуждать по карте от начальной точке n раз. Также может влиять то, что время работы алгоритма зависит от положения станций.
В этой главе мы реализовали алгоритм эвристического поиска А*. Также мы узнали несколько стандартных структур данных. Это множества и очереди с приоритетом и освежили в памяти ленивые вычисления.
Мы научились проверять свойства программ (QuickCheck), а также оценивать быстродействие программ (criterion).
Я говорил о том, что два варианта алгоритмов дают одинаковые результаты, но так ли это на самом деле? Проверьте это в QuickCheck.
Алгоритм эвристического поиска может применяться не только для поиска маршрутов на карте. Часто алгоритм А* применяется в играх. Встройте этот алгоритм в игру пятнашки (глава 13). Если игрок запутался и не знает как ходить, он может попросить у компьютера совет. В этой задаче альтернативы~– это вершины графа, соседние вершины~– это те вершины, в которые мы можем попасть за один ход.
Подсказка: воспользуйтесь манхэттенским расстоянием.
Оцените эффективность двух алгоритмов поиска в игре пятнашки. Рассмотрите зависимость быстродействия от степени сложности игры.