Граф
С помощью типов мы определяем все возможные значения в нашей программе. Мы определяем основные примитивы и способы их комбинирования. Например в типе Nat:
data Nat = Zero | Succ Nat
Один конструктор-примитив Zero, и один конструктор Succ, с помощью которого мы можем делать составные значения. Определив тип Nat таким образом, мы говорим, что значения типа Nat могут быть только такими:
Zero, Succ Zero, Succ (Succ Zero), Succ (Succ (Succ Zero)), ...
Все значения являются цепочками Succ с Zero на конце. Если где-нибудь мы попытаемся построить значение, которое не соответствует нашему типу, мы получим ошибку компиляции, то есть программа не пройдёт проверку типов. Так типы описывают множество допустимых значений.
Значения, которые проходят проверку типов мы будем называть допустимыми, а те, которые не проходят соответственно недопустимыми. Так например следующие значения недопустимы для Nat
Succ Zero Zero, Succ Succ, True, Zero (Zero Succ), ...
Недопустимых значений конечно гораздо больше. Такое проявляется и в естественном языке, бессмысленных комбинаций слов гораздо больше, чем осмысленных предложений. Обратите внимание на то, что мы говорим о значениях (не)допустимых для некоторого типа, например значение True допустимо для Bool, но недопустимо для Nat.
Сами типы строятся не произвольным образом. Мы узнали, что при их построении используются две основные операции, это сумма и произведение типов. Это говорит о том, что в типах должны быть какие-то закономерности, которые распространяются на все значения. В этой главе мы посмотрим на эти закономерности.
Итак у нас лишь две операции: сумма и произведение. Давайте для начала рассмотрим два крайних случая.
Только произведение типов
data T = Name T1 T2 ... TN
Мы говорим, что значение нашего нового типа T состоит из значений типов T1, T2, … , TN и у нас есть лишь один способ составить значение этого типа. Единственное, что мы можем сделать это применить к значениям типов Ti конструктор Name.
Пример:
data Time = Time Hour Second Minute
Только сумма типов
data T = Name1 | Name2 | ... | NameN
Мы говорим, что у нашего нового типа T может быть лишь несколько значений, и перечисляем их в альтернативах через знак |.
Пример:
data Bool = True | False
Сделаем первое наблюдение: каждое произведение типов определяет новый конструктор. Число конструкторов в типе равно числу альтернатив. Так в первом случае у нас была одна альтернатива и следовательно у нас был лишь один конструктор Name.
Имена конструкторов должны быть уникальными в пределах модуля. У нас нет таких двух типов, у которых совпадают конструкторы. Это говорит о том, что по имени конструктора компилятор знает значение какого типа он может построить.
Произведение типов состоит из конструктора, за которым через пробел идут подтипы. Такая структура не случайна, она копирует структуру функции. В качестве имени функции выступает конструктор, а в качестве аргументов – значения заданных в произведении подтипов. Функция-конструктор после применения “оборачивает” значения аргументов и создаёт новое значение. За счёт этого мы могли бы определить типы по-другому. Мы могли бы определить их в стиле классов типов:
data Bool where
True :: Bool
False :: Bool
Мы видим “класс” Bool, у которого два метода. Или определим в таком стиле Nat:
data Nat where
Zero :: Nat
Succ :: Nat -> Nat
Мы переписываем подтипы по порядку в аргументы метода. Или определим в таком стиле списки:
data [a] where
[] :: [a]
(:) :: a -> [a] -> [a]
Конструктор пустого списка [] является константой, а конструктор объединения элемента со списком (:), является функцией. Когда я говорил, что типы определяют примитивы и методы составления из примитивов, я имел ввиду, что некоторые конструкторы по сути являются константами, а другие функциями. Эти “методы” определяют базовые значения типа, все другие значения будут комбинациями базовых.
Мы уже знаем, что значения могут быть функциями и константами. Объявляя константу, мы даём имя-синоним некоторой комбинации базовых конструкторов. В функции мы говорим как по одним значениям получить другие. В этом и следующем разделе мы посмотрим на то, как типы определяют структуру констант и функций.
Давайте присмотримся к константам:
Succ (Succ Zero) Neg (Add One (Mul Six Ten)) Not (Follows A (And A B)) Cons 1 (Cons 2 (Cons 3 (Cons 4 Nil)))
Заменим все функциональные конструкторы на букву f (от слова function), а все примитивные конструкторы на букву c (от слова constant).
f (f c) f (f c (f c c)) f (f c (f c c)) f c (f c (f c (f c c)))
Те кто знаком с теорией графов, возможно уже узнали в этой записи строчную запись дерева. Все значения в Haskell являются деревьями. Узел дерева содержит составной конструктор, а лист дерева содержит примитивный конструктор. Далее будет небольшой подраздел посвящённый терминологии теории графов, которая нам понадобится, будет много картинок, если вам это известно, то вы можете спокойно его пропустить.
Если вы не знакомы с теорией графов, то сейчас как раз самое время с ней познакомится, хотя бы на уровне основных терминов. Теория графов изучает дискретные объекты в терминах зависимостей между объектами или связей. При этом объекты и связи можно изобразить графически.
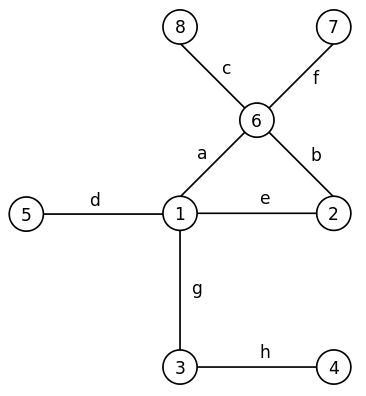
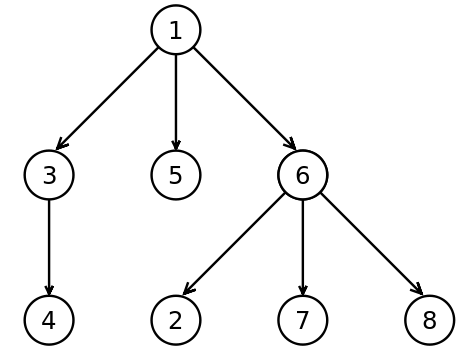
Граф состоит из узлов и рёбер, которые соединяют узлы. Приведём пример графа:

Граф
В этом графе восемь узлов, они пронумерованы, и восемь рёбер, они обозначены буквами. Теорию графов придумал Леонард Эйлер, когда решал задачу о кёнингсбергских мостах. Он решал задачу о том, можно ли обойти все семь кёнингсбергских мостов так, чтобы пройти по каждому лишь один раз. Эйлер представил мосты в виде рёбер а участки суши в виде узлов графа и показал, что это сделать нельзя. Но мы отвлеклись.
А что такое дерево? Дерево это такой связанный граф, у которого нет циклов. Несвязанный граф образует несколько островков, или множеств узлов, которые не соединены рёбрами. Циклы – это замкнутые последовательности рёбер. Например граф на рисунке выше не является деревом, но если мы сотрём ребро e, то у нас получится дерево.
Ориентированный граф – это такой граф, у которого все рёбра являются стрелками, они ориентированы, отсюда и название. При этом теперь каждое ребро не просто связывает узлы, но имеет начало и конец. В ориентированных деревьях обычно выделяют один узел, который называют корнем. Его особенность заключается в том, что все стрелки в ориентированном дереве как бы “разбегаются” от корня или сбегаются к корню. Корень определяет все стрелки в дереве. Ориентированное дерево похоже на иерархию. У нас есть корневой элемент и набор его дочерних поддеревьев, каждое из поддеревьев в свою очередь является ориентированным деревом и так далее. Проиллюстрируем на картинке, давайте сотрём ребро e и назначим первый узел корнем. Все наши стрелки будут идти от корня. Сначала мы проведём стрелки к узлам связанным с корнем:
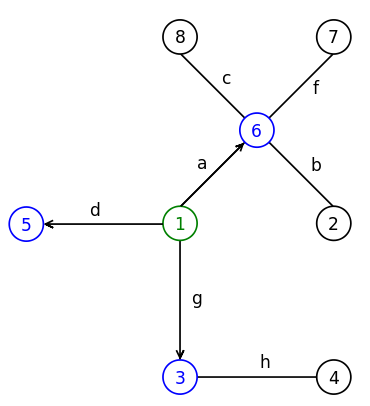
Превращаем в дерево
Затем представим, что каждый из этих узлов сам является корнем в своём дереве и повторим эту процедуру. На этом шаге мы дорисовываем стрелки в поддеревьях, которые находятся в узлах 3 и 6. Узел 5 является вырожденным деревом, в нём всего лишь одна вершина. Мы будем называть такие поддеревья листьями. А невырожденные поддеревья мы будем называть узлами. Корневой узел в данном поддереве называют родительским. А его соседние узлы, в которые направлены исходящие из него стрелки называют дочерними узлами. На предыдущем шаге у нас появился один родительский узел 1, у которого три дочерних узла: 3, 6, и 5. А на этом шаге у нас появились ещё два родительских узла 3 и 6. У узла 3 один дочерний узел (4), а у узла 6 – три дочерних узла (2, 8, 7).
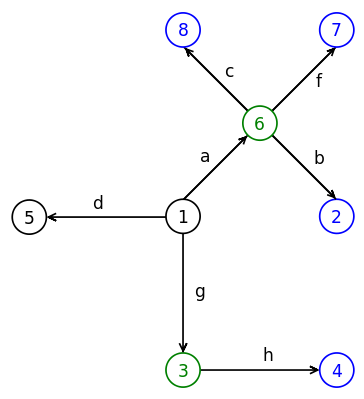
Превращаем в дерево…
Отметим, что положение узлов и рёбер на картинке не важно, главное это то, какие рёбра какие узлы соединяют. Мы можем перерисовать это дерево в более привычном виде.
Теперь если вы посмотрите на константы в Haskell вы заметите, что очень похожи на деревья. Листья содержат примитивные конструкторы, а узлы – составные. Это происходит из-за того, что каждый конструктор содержит метку и набор подтипов. В этой аналогии метки становятся узлами, а подтипы-аргументы становятся поддеревьями.
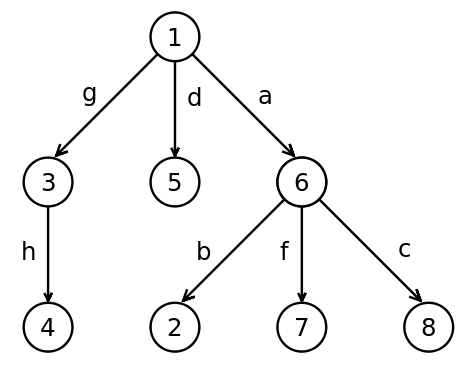
Ориентированное дерево
Но есть одна тонкость, в которой заключается отличие констант Haskell от деревьев из теории графов. В теории графов порядок поддеревьев не важен, мы могли бы нарисовать поддеревья в любом порядке, главное сохранить связи. А в Haskell порядок следования аргументов в конструкторе важен.
На следующем рисунке изображены две константы:Succ (Succ Zero) :: Nat и Neg (Add One (Mul Six Ten)) :: Expr. Но они изображены немного по-другому. Я перевернул стрелки и добавил корнем ещё один узел, это тип константы.
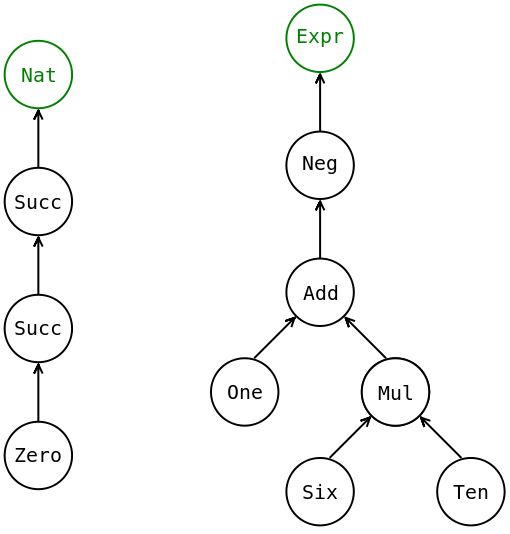
Константы
Стрелки перевёрнуты так, чтобы стрелки на картинке соответствовали стрелкам в типе конструктора. Например по виду узла Succ :: Nat -> Nat, можно понять, что это функция от одного аргумента, в неё впадает одна стрелка-аргумент и вытекает одна стрелка-значение. В конструктор Mul впадает две стрелки, значит это конструктор-функция от двух аргументов.
Константы похожи на деревья за счёт структуры операции произведения типов. В произведении типов мы пишем:
data Tnew = New T1 T2 ... Tn
Так и получается, что у нашего узла New одна вытекающая стрелка, которая символизирует значение типа Tnew и несколько впадающих стрелок T1, T2, …, Tn, они символизируют аргументы конструктора.
Потренируйтесь изображать константы в виде деревьев, вспомните константы из предыдущей главы, или придумайте какие-нибудь новые.
Итак все константы в Haskell за счёт особой структуры построения типов являются деревьями, но мы программируем в текстовом редакторе, а не в редакторе векторной графики, поэтому нам нужен удобный способ строчной записи дерева. Мы им уже активно пользуемся, но сейчас давайте опишем его по-подробнее.
Мы сидим на корне дерева и спускаемся по его вершинам. Нам могут встретиться вершины двух типов узлы и листья. Сначала мы пишем имя в текущем узле, затем через пробел имена в дочерних узлах, если нам встречается невырожденный узел мы заключаем его в скобки. Давайте последовательно запишем в строчной записи дерево из первого примера:
Ориентированное дерево
Начнём с корня и будем последовательно дописывать поддеревья, точками обозначаются дочерние узлы, которые нам ещё предстоит дописать:
(1 . . . ) (1 (3 .) 5 (6 . . .)) (1 (3 4) 5 (6 2 7 8))
Мы можем ставить любое число пробелов между дочерними узлами, здесь для наглядности точки выровнены. Так мы можем закодировать исходное дерево строкой. Часто самые внешние скобки опускаются. В итоге получилась такая запись:
tree = 1 (3 4) 5 (6 2 7 8)
По этой записи мы можем понять, что у нас есть два конструктора трёх аргументов 1 и 6, один конструктор одного аргумента 3 и пять примитивных конструкторов. Точно так же мы строим и все другие константы в Haskell:
Succ (Succ (Succ Zero)) Time (Hour 13) (Minute 10) (Second 0) Mul (Add One Ten) (Neg (Mul Six Zero))
За одним исключением, если конструктор бинарный, символьный (начинается с двоеточия), мы помещаем его между аргументов:
(One :+ Ten) :* (Neg (Six :* Zero))
Теперь мы разобрались с тем, что константы это деревья. Значит функции строят одни деревья из других. Как они это делают? Для этого в Haskell есть две операции: это композиция и декомпозиция деревьев. С помощью композиции мы строим из простых деревьев сложные, а с помощью декомпозиции разбиваем составные деревья на простейшие.
Композиция и декомпозиция объединены в одной операции, с которой мы уже встречались, это операция определения синонима. Давайте вспомним какое-нибудь объявление функции:
(+) a Zero = a (+) a (Succ b) = Succ (a + b)
Смотрите в этой функции слева от знака равно мы проводим декомпозицию второго аргумента, а в правой части мы составляем новое дерево из тех значений, что были нами получены слева от знака равно. Или посмотрим на другой пример:
show (Time h m s) = show h ++ ":" ++ show m ++ ":" ++ show s
Слева от знака равно мы также выделили из составного дерева (Time h m s) три его дочерних для корня узла и связали их с переменными h, m и s. А справа от знака равно мы составили из этих переменных новое выражение.
Итак операцию объявления синонима можно представить в таком виде:
name декомпозиция = композиция
В каждом уравнении у нас три части: новое имя, декомпозиция, поступающих на вход аргументов, и композиция нового значения. Остановимся поподробнее на каждой из этих операций.
Композиция строится по очень простому правилу, если у нас есть значение f типа a -> b и значение x типа a, мы можем получить новое значение (f x) типа b. Это основное правило построения новых значений, поэтому давайте запишем его отдельно:
f :: a -> b, x :: a
--------------------------
(f x) :: b
Сверху от черты, то что у нас есть, а снизу от черты то, что мы можем получить. Это операция называется применением или аппликацией.
Выражения, полученные таким образом, напоминают строчную запись дерева, но есть одна тонкость, которую мы обошли стороной. В случае деревьев мы строили только константы, и конструктор получал столько аргументов, сколько у него было дочерних узлов (или подтипов). Так мы строили константы. Но в Haskell мы можем с помощью применения строить функции на лету, передавая меньшее число аргументов, этот процесс называется частичным применением или каррированием (currying). Поясним на примере, предположим у нас есть функция двух аргументов:
add :: Nat -> Nat -> Nat add a b = ...
На самом деле компилятор воспринимает эту запись так:
add :: Nat -> (Nat -> Nat) add a b = ...
Функция add является функцией одного аргумента, которая в свою очередь возвращает функцию одного аргумента (Nat -> Nat). Когда мы пишем в где-нибудь в правой части функции:
... = ... (add Zero (Succ Zero)) ...
Компилятор воспринимает эту запись так:
... = ... ((add Zero) (Succ Zero)) ...
Присмотримся к этому выражению, что изменилось? У нас появились новые скобки, вокруг выражения (add Zero). Давайте посмотрим как происходит применение:
add :: Nat -> (Nat -> Nat), Zero :: Nat
----------------------------------------------
(add Zero) :: Nat -> Nat
Итак применение функции add к Zero возвращает новую функцию (add Zero), которая зависит от одного аргумента. Теперь применим к этой функции второе значение:
(add Zero) :: Nat -> Nat, (Succ Zero) :: Nat
----------------------------------------------
((add Zero) (Succ Zero)) :: Nat
И только теперь мы получили константу. Обратите внимание на то, что получившаяся константа не может принять ещё один аргумент. Поскольку в правиле для применения функция f должна содержать стрелку, а у нас есть лишь Nat, это значение может участвовать в других выражениях лишь на месте аргумента.
Тоже самое работает и для функций от большего числа аргументов, если мы пишем
fun :: a1 -> a2 -> a3 -> a4 -> res ... = fun a b c d
На самом деле мы пишем
fun :: a1 -> (a2 -> (a3 -> (a4 -> res))) ... = (((fun a) b) c) d
Это очень удобно. Так, определив лишь одну функцию fun, мы получили в подарок ещё три функции (fun a), (fun a b) и (fun a b c). С ростом числа аргументов растёт и число подарков. Если смотреть на функцию fun, как на функцию одного аргумента, то она представляется таким генератором функций типа a2 -> a3 -> a4 -> res, который зависит от параметра. Применение функций через пробел значительно упрощает процесс комбинирования функций.
Поэтому в Haskell аргументы функций, которые играют роль параметров или специфических флагов, то есть аргументы, которые меняются редко обычно пишутся в начале функции. Например
process :: Param1 -> Param2 -> Arg1 -> Arg2 -> Result
Два первых аргумента функции process выступают в роли параметров для генерации функций с типом Arg1 -> Arg2 -> Result.
Давайте потренируемся с частичным применением в интерпретаторе. Для этого загрузим модуль Nat из предыдущей главы:
Prelude> :l Nat [1 of 1] Compiling Nat ( Nat.hs, interpreted ) Ok, modules loaded: Nat. *Nat> let add = (+) :: Nat -> Nat -> Nat *Nat> let addTwo = add (Succ (Succ Zero)) *Nat> :t addTwo addTwo :: Nat -> Nat *Nat> addTwo (Succ Zero) Succ (Succ (Succ Zero)) *Nat> addTwo (addTwo Zero) Succ (Succ (Succ (Succ Zero)))
Сначала мы ввели локальную переменную add, и присвоили ей метод (+) из класса Num для Nat. Нам пришлось выписать тип функции, поскольку ghci не знает для какого экземпляра мы хотим определить этот синоним. В данном случае мы подсказали ему, что это Nat. Затем с помощью частичного применения мы объявили новый синоним addTwo, как мы видим из следующей строки это функция оного аргумента. Она принимает любое значение типа Nat и прибавляет к нему двойку. Мы видим, что этой функцией можно пользоваться также как и обычной функцией.
Попробуем выполнить тоже самое для функции с символьной записью имени:
*Nat> let add2 = (+) (Succ (Succ Zero)) *Nat> add2 Zero Succ (Succ Zero)
Мы рассмотрели частичное применение для функций в префиксной форме записи. В префиксной форме записи функция пишется первой, затем следуют аргументы. Для функций в инфиксной форме записи существует два правила применения.
Это применение слева:
(*) :: a -> (b -> c), x :: a
-----------------------------
(x *) :: b -> c
И применение справа:
(*) :: a -> (b -> c), x :: b
-----------------------------
(* x) :: a -> c
Обратите внимание на типы аргумента и возвращаемого значения. Скобки в выражениях (x*) и (*x) обязательны. Применением слева мы фиксируем в бинарной операции первый аргумент, а применением справа – второй.
Поясним на примере, для этого давайте возьмём функцию минус (-). Если мы напишем (2-) 1 то мы получим 1, а если мы напишем (-2) 1, то мы получим -1. Проверим в интерпретаторе:
*Nat> (2-) 1
1
*Nat> (-2) 1
<interactive>:4:2:
No instance for (Num (a0 -> t0))
arising from a use of syntactic negation
Possible fix: add an instance declaration for (Num (a0 -> t0))
In the expression: - 2
In the expression: (- 2) 1
In an equation for `it': it = (- 2) 1
Ох уж этот минус. Незадача. Ошибка произошла из-за того, что минус является хамелеоном. Если мы пишем -2, компилятор воспринимает минус как унарную операцию, и думает, что мы написали константу минус два. Это сделано для удобства, но иногда это мешает. Это единственное такое исключение в Haskell. Давайте введём новый синоним для операции минус:
*Nat> let (#) = (-) *Nat> (2#) 1 1 *Nat> (#2) 1 -1
Эти правила левого и правого применения работают и для буквенных имён в инфиксной форме записи:
*Nat> let minus = (-) *Nat> (2 `minus` ) 1 1 *Nat> ( `minus` 2) 1 -1
Так если мы хотим на лету получить новую функцию, связав в функции второй аргумент мы можем написать:
... = ... ( `fun` x) ...
Частичное применение для функций в инфиксной форме записи называют сечением (section), они бывают соответственно левыми и правыми.
Отметим связь основного правила применения с Modus Ponens, известным правилом вывода в логике:
a -> b, a
-------------
b
Оно говорит о том, что если у нас есть выражение из a следует b и мы знаем, что a истинно, мы смело можем утверждать, что b тоже истинно. Если перевести это правило на Haskell, то мы получим: Если у нас определена функция типа a -> b и у нас есть значение типа a, то мы можем получить значение типа b.
Декомпозиция применяется слева от знака равно, при этом наша задача состоит в том, чтобы опознать дерево определённого вида и выделить из него некоторые поддеревья. Мы уже пользовались декомпозицией много раз в предыдущих главах, давайте выпишем примеры декомпозиции:
not :: Bool -> Bool not True = ... not False = ... xor :: Bool -> Bool -> Bool xor a b = ... show :: Show a => a -> String show (Time h m s) = ... addZero :: String -> String addZero (a:[]) = ... addZero as = ... (*) a Zero = ... (*) a (Succ b) = ...
Декомпозицию можно проводить в аргументах функции. Там мы видим строчную запись дерева, в узлах стоят конструкторы (начинаются с большой буквы), переменные (с маленькой буквы) или символ безразличной переменой (подчёркивание).
С помощью конструкторов, мы указываем те части, которые обязательно должны быть в дереве для данного уравнения. Так уравнение
not True = ...
сработает, только если на вход функции поступит значение True. Мы можем углубляться в дерево значения настолько, насколько нам позволят типы, так мы можем определить функцию:
is7 :: Nat -> Bool is7 (Succ (Succ (Succ (Succ (Succ (Succ (Succ Zero))))))) = True is7 _ = False
С помощью переменных мы даём синонимы поддеревьям. Этими синонимами мы можем пользоваться в правой части функции. Так в уравнении
addZero (a:[])
мы извлекаем первый элемент из списка, и одновременно говорим о том, что список может содержать только один элемент. Отметим, что если мы хотим дать синоним всему дереву а не какой-то части, мы просто пишем на месте аргумента переменную, как в случае функции xor:
xor a b = ...
С помощью безразличной переменной говорим, что нам не важно, что находится у дерева в этом узле. Уравнения в определении синонима обходятся сверху вниз, поэтому часто безразличной переменной пользуются в смысле “а во всех остальных случаях”, как в:
instance Eq Nat where
(==) Zero Zero = True
(==) (Succ a) (Succ b) = a == b
(==) _ _ = False
Переменные и безразличные переменные также могут уходить вглубь дерева сколь угодно далеко (или ввысь дерева, поскольку первый уровень в строчной записи это корень):
lessThan7 :: Nat -> Bool lessThan7 (Succ (Succ (Succ (Succ (Succ (Succ (Succ _))))))) = False lessThan7 _ = True
Декомпозицию можно применять только к значениям-константам. Проявляется интересная закономерность: если для композиции необходимым элементом было значение со стрелочным типом (функция), то в случае декомпозиции нам нужно значение с типом без стрелок (константа). Это говорит о том, что все функции будут полностью применены, то есть константы будут записаны в виде строчной записи дерева. Если мы ожидаем на входе функцию, то мы можем только дать ей синоним с помощью с помощью переменной или проигнорировать её безразличной переменной.
Как в
name (Succ (Succ Zero)) = ... name (Zero : Succ Zero : []) = ...
Но не
name Succ = ... name (Zero :) = ...
Отметим, что для композиции это допустимые значения, в первом случае это функция Nat -> Nat, а во втором это функция типа [Nat] -> [Nat].
Ещё одна особенность декомпозиции заключается в том, что при декомпозиции мы можем пользоваться только “настоящими” значениями, то есть конструкторами, объявленными в типах. В случае композиции мы могли пользоваться как конструкторами, так и синонимами.
Например мы не можем написать в декомпозиции:
name (add Zero Zero) = ... name (or (xor a b) True) = ...
В Haskell декомпозицию принято называть сопоставлением с образцом (pattern matching). Термин намекает на то, что в аргументе мы выписываем шаблон (или заготовку) для целого набора значений. Наборы значений могут получиться, если мы пользуемся переменными. Конструкторы дают нам возможность зафиксировать вид ожидаемого на вход дерева.
В этом разделе мы поговорим об ошибках проверки типов. Почти все ошибки, которые происходят в Haskell, связаны с проверкой типов. Проверка типов происходит согласно правилам применения, которые встретились нам в разделе о композиции значений. Мы остановимся лишь на случае для префиксной формы записи, правила для сечений работают аналогично. Давайте вспомним основное правило:
f :: a -> b, x :: a
--------------------------
(f x) :: b
Что может привести к ошибке? В этом правиле есть два источника ошибки.
Тип f не содержит стрелок, или f не является функцией.
Типы x и аргумента для f не совпадают.
Вот и все ошибки. Универсальное представление всех функций в виде функций одного аргумента, значительно сокращает число различных видов ошибок. Итак мы можем ошибиться, применяя значение к константе и передав в функцию не то, что она ожидает.
Потренируемся в интерпретаторе, сначала попытаемся создать ошибку первого типа:
*Nat> Zero Zero
<interactive>:1:1:
The function `Zero' is applied to one argument,
but its type `Nat' has none
In the expression: Zero Zero
In an equation for `it': it = Zero Zero
Если перевести на русский интерпретатор говорит:
*Nat> Zero Zero
<interactive>:1:1:
Функция 'Zero' применяется к одному аргументу,
но её тип 'Nat' не имеет аргументов
В выражении: Zero Zero
В уравнении для `it': it = Zero Zero
Компилятор увидел применение функции f x, далее он посмотрел, что x = Zero, из этого на основе правила применения он сделал вывод о том, что f имеет тип Nat -> t, тогда он заглянул в f и нашёл там Zero :: Nat, что и привело к несовпадению типов.
Перейдём к ошибкам второго типа. Попробуем вызывать функции с неправильными аргументами:
*Nat> :m +Prelude
*Nat Prelude> not (Succ Zero)
<interactive>:9:6:
Couldn't match expected type `Bool' with actual type `Nat'
In the return type of a call of `Succ'
In the first argument of `not', namely `(Succ Zero)'
In the expression: not (Succ Zero)
Опишем действия компилятора в терминах правила применения. В этом выражении у нас есть три значения: not, Succ и Zero. Нам нужно узнать тип выражения и проверить правильно ли оно построено.
not (Succ Zero) - ?
not :: Bool -> Bool, Succ :: Nat -> Nat, Zero :: Nat
----------------------------------------------------------
f x, f = not и x = (Succ Zero)
------------------------------------------------------------
f :: Bool -> Bool следовательно x :: Bool
-------------------------------------------------------------
(Succ Zero) :: Bool
Воспользовавшись правилом применения мы узнали, что тип выражения Succ Zero должен быть равен Bool. Проверим, так ли это?
(Succ Zero) - ?
Succ :: Nat -> Nat, Zero :: Nat
----------------------------------------------------------
f x, f = Succ, x = Zero следовательно (f x) :: Nat
----------------------------------------------------------
(Succ Zero) :: Nat
Из этой цепочки следует, что (Succ Zero) имеет тип Nat. Мы пришли к противоречию и сообщаем об этом пользователю.
<interactive>:1:5:
Не могу сопоставить ожидаемый тип 'Bool' с выведенным 'Nat'
В типе результата вызова `Succ'
В первом аргументе `not', а именно `(Succ Zero)'
В выражении: not (Succ Zero)
Потренируйтесь в составлении неправильных выражений и посмотрите почему они не правильные. Мысленно сверьтесь с правилом применения в каждом из слагаемых.
Мы говорили о том, что тип аргумента функции и тип подставляемого значения должны совпадать, но на самом деле есть и другая возможность. Тип аргумента или тип значения могут быть полиморфными. В этом случае происходит специализация общего типа. Например, при выполнении выражения:
*Nat> Succ Zero + Zero Succ (Succ Zero)
Происходит специализация общей функции (+) :: Num a => a -> a -> a до функции (+) :: Nat -> Nat -> Nat, которая определена в экземпляре Num для Nat.
Предположим, что у функции f есть контекст, который говорит о том, что первый аргумент принадлежит некоторому классу f :: C a => a -> b, тогда значение, которое мы подставляем в функцию, должно быть экземпляром класса C.
Для иллюстрации давайте попробуем сложить логические значения:
*Nat Prelude> True + False
<interactive>:11:6:
No instance for (Num Bool)
arising from a use of `+'
Possible fix: add an instance declaration for (Num Bool)
In the expression: True + False
In an equation for `it': it = True + False
Компилятор говорит о том, что для типа Bool не
определён экземпляр для класса Num.
No instance for (Num Bool)
Запишем это в виде правила:
f :: C a => a -> b, x :: T, instance C T
-----------------------------------------
(f x) :: b
Важно отметить, что x имеет конкретный тип T. Если x – значение, у которого тип с параметром, компилятор не сможет определить для какого типа конкретно мы хотим выполнить применение. Мы будем называть такую ситуацию неопределённостью:
x :: T a => a f :: C a => a -> b f x :: ?? -- неопределённость
Мы видим, что тип x, это какой-то тип, одновременно принадлежащий и классу T и классу C. Но мы не можем сказать какой это тип. У этого поведения есть исключение: по умолчанию числа приводятся к Integer, если они не содержат знаков после точки, и к Double – если содержат.
*Nat Prelude> let f = (1.5 + ) *Nat Prelude> :t f f :: Double -> Double *Nat Prelude> let x = 5 + 0 *Nat Prelude> :t x x :: Integer *Nat Prelude> let x = 5 + Zero *Nat Prelude> :t x x :: Nat
Умолчания определены только для класса Num. Для этого есть специальное ключевое слово default. В рамках модуля мы можем указать какие типы считаются числами по умолчанию. Например, так (такое умолчание действует в каждом модуле, но мы можем переопределить его):
default (Integer, Double)
Работает правило: если произошла неопределённость и один из участвующих классов является Num, а все остальные классы – это стандартные классы, определённые в Prelude, то компилятор начинает последовательно пробовать все типы, перечисленные за ключевым словом default, пока один из них не подойдёт. Если такого типа не окажется, компилятор скажет об ошибке.
С выводом типов в классах связана одна тонкость. Мы говорили, что не обязательно выписывать типы выражений, компилятор может вывести их самостоятельно. Например, мы постоянно пользуемся этим в интерпретаторе. Также когда мы говорили о частичном применении, мы сказали об очень полезном умолчании в типах функций. О том, что за счёт частичного применения, все функции являются функциями одного аргумента. Эта особенность позволяет записывать выражения очень кратко. Но иногда они получаются чересчур краткими, и вводят компилятор в заблуждение. Зайдём в интерпретатор:
Prelude> let add = (+) Prelude> :t add add :: Integer -> Integer -> Integer
Мы хотели определить синоним для метода плюс из класса Num, но вместо ожидаемого общего типа получили более частный. Сработало умолчание для численного типа. Но зачем оно сработало? Если мы попробуем дать синоним методу из класса Eq, ситуация станет ещё более странной:
Prelude> let eq = (==) Prelude> :t eq eq :: () -> () -> Bool
Мы получили какую-то ерунду. Если мы попытаемся загрузить модуль с этими определениями:
module MR where add = (+) eq = (==)
то получим:
*MR> :l MR
[1 of 1] Compiling MR ( MR.hs, interpreted )
MR.hs:4:7:
Ambiguous type variable `a0' in the constraint:
(Eq a0) arising from a use of `=='
Possible cause: the monomorphism restriction applied to the following:
eq :: a0 -> a0 -> Bool (bound at MR.hs:4:1)
Probable fix: give these definition(s) an explicit type signature
or use -XNoMonomorphismRestriction
In the expression: (==)
In an equation for `eq': eq = (==)
Failed, modules loaded: none.
Компилятор жалуется о том, что в определении для eq ему встретилась неопределённость и он не смог вывести тип. Если же мы допишем недостающие типы:
module MR where add :: Num a => a -> a -> a add = (+) eq :: Eq a => a -> a -> Bool eq = (==)
то всё пройдёт гладко:
Prelude> :l MR [1 of 1] Compiling MR ( MR.hs, interpreted ) Ok, modules loaded: MR. *MR> eq 2 3 False
Но оказывается, что если мы допишем аргументы у функций и сотрём объявления, компилятор сможет вывести тип, и тип окажется общим. Это можно проверить в интерпретаторе. Для этого начнём новую сессию:
Prelude> let eq a b = (==) a b Prelude> :t eq eq :: Eq a => a -> a -> Bool Prelude> let add a = (+) a Prelude> :t add add :: Num a => a -> a -> a
Запишите эти выражения в модуле без типов и попробуйте загрузить. Почему так происходит? По смыслу определения
add a b = (+) a b add = (+)
ничем не отличаются друг от друга, но второе сбивает компилятор столку. Компилятор путается из-за того, что второй вариант похож на определение константы. Мы с вами знаем, что выражение справа от знака равно является функцией, но компилятор, посчитав аргументы слева от знака равно, думает, что это возможно константа, потому что она выглядит как константа. У таких возможно-констант есть специальное имя, они называются константными аппликативными формами (constant applicative form или сокращённо CAF). Константы можно вычислять один раз, на то они и константы. Но если тип константы перегружен, и мы не знаем что это за тип (если пользователь не подсказал нам об этом в объявлении типа), то нам приходится вычислять его каждый раз заново. Посмотрим на пример:
res = s + s s = someLongLongComputation 10 someLongLongComputation :: Num a => a -> a
Здесь значение s содержит результат вычисления какой-то большой-пребольшой функции. Перед компилятором стоит задача вывода типов. По тексту можно определить, что у s и res некоторый числовой тип. Проблема в том, что поскольку компилятор не знает какой тип у s конкретно в выражении s + s, он вынужден вычислить s дважды. Это привело разработчиков Haskell к мысли о том, что все выражения, которые выглядят как константы должны вычисляться как константы, то есть лишь один раз. Это ограничение называют ограничением мономорфизма. По умолчанию все константы должны иметь конкретный тип, если только пользователь не укажет обратное в типе или не подскажет компилятору косвенно, подставив неопределённое значение в другое значение, тип которого определён. Например, такой модуль загрузится без ошибок:
eqToOne = eq one eq = (==) one :: Int one = 1
Только в этом случае мы не получим общего типа для eq: компилятор постарается вывести значение, которое не содержит контекста. Поэтому получится, что функция eq определена на Int. Эта очень спорная особенность языка, поскольку на практике получается так, что ситуации, в которых она мешает, возникают гораздо чаще. Немного забегая вперёд, отметим, что это поведение компилятора по умолчанию, и его можно изменить. Компилятор даже подсказал нам как это сделать в сообщении об ошибке:
Probable fix: give these definition(s) an explicit type signature
or use -XNoMonomorphismRestriction
Мы можем активировать расширение языка, которое отменяет это ограничение. Сделать это можно несколькими способами. Мы можем запустить интерпретатор с флагом -XNoMonomorphismRestriction:
Prelude> :q Leaving GHCi. $ ghci -XNoMonomorphismRestriction Prelude> let eq = (==) Prelude> :t eq eq :: Eq a => a -> a -> Bool
или в самом начале модуля написать:
{-# Language NoMonomorphismRestriction #-}
Расширение будет действовать только в рамках данного модуля.
Обсудим ещё одну особенность системы типов Haskell. Типы могут быть рекурсивными, то есть одним из подтипов в определении типа может быть сам определяемый тип. Мы уже пользовались этим в определении для Nat
data Nat = Zero | Succ Nat
Видите, во второй альтернативе участвует сам тип Nat. Это приводит к бесконечному числу значений. Таким простым и коротким определением мы описываем все положительные числа. Рекурсивные определения типов приводят к рекурсивным функциям. Помните, мы определяли сложение и умножение:
(+) a Zero = a (+) a (Succ b) = Succ (a + b) (*) a Zero = Zero (*) a (Succ b) = a + (a * b)
И та и другая функция получились рекурсивными. Они следуют по одному сценарию: сначала определяем базу рекурсии~– тот случай, в котором мы заканчиваем вычисление функции, и затем определяем путь к базе~– цепочку рекурсивных вызовов.
Рассмотрим тип по-сложнее. Списки:
data [a] = [] | a : [a]
Деревья значений для Nat напоминают цепочку конструкторов Succ, которая венчается конструктором Zero. Дерево значений для списка отличается лишь тем, что теперь у каждого конструктора Succ есть отросток, который содержит значение некоторого типа a. Значение заканчивается пустым списком [].
Мы можем предположить, что функции для списков также будут рекурсивными. Это и правда так. Посмотрим на три основные функции для списков. Все они определены в Prelude. Начнём с функции преобразования всех элементов списка:
map :: (a -> b) -> [a] -> [b]
Посмотрим как она работает:
Prelude> map (+100) [1,2,3] [101,102,103] Prelude> map not [True, True, False, False, False] [False,False,True,True,True] Prelude> :m +Data.Char Prelude Data.Char> map toUpper "Hello World" "HELLO WORLD"
Теперь опишем эту функцию. Базой рекурсии будет случай для пустого списка. В нём мы говорим, что если элементы закончились, нам нечего больше преобразовывать, и возвращаем пустой список. Во втором уравнении нам встретится узел дерева, который содержит конструктор :, а в дочерних узлах сидят элемент списка a и оставшаяся часть списка as. В этом случае мы составляем новый список, элемент которого содержит преобразованный элемент (f a) исходного списка и оставшуюся часть списка, которую мы также преобразуем с помощью функции map:
map :: (a -> b) -> [a] -> [b] map f [] = [] map f (a:as) = f a : map f as
Какое длинное объяснение для такой короткой функции! Надеюсь, что мне не удалось сбить вас с толку. Обратите внимание на то, что поскольку конструктор символьный (начинается с двоеточия) мы пишем его между дочерними поддеревьями, а не сначала. Немного отвлекитесь и поэкспериментируйте с этой функцией в интерпретаторе, она очень важная. Составляйте самые разные списки. Чтобы не перенабирать каждый раз списки водите синонимы с помощью let.
Перейдём к следующей функции. Это функция фильтрации:
filter :: (a -> Bool) -> [a] -> [a]
Она принимает предикат и список. Угадайте, что она делает:
Prelude Data.Char> filter isUpper "Hello World" "HW" Prelude Data.Char> filter even [1,2,3,4,5] [2,4] Prelude Data.Char> filter (>10) [1,2,3,4,5] []
Да, она оставляет лишь те элементы, на которых предикат вернёт истину. Потренируйтесь и с этой функцией.
Теперь определение:
filter :: (a -> Bool) -> [a] -> [a] filter p [] = [] filter p (x:xs) = if p x then x : filter p xs else filter p xs
Попробуйте разобраться с ним самостоятельно, по аналогии с map. Оно может показаться немного громоздким, но это ничего, совсем скоро мы узнаем как записать его гораздо проще.
Рассмотрим ещё одну функцию для списков, она называется функцией свёртки:
foldr :: (a -> b -> b) -> b -> [a] -> b foldr f z [] = z foldr f z (a:as) = f a (foldr f z as)
Визуально её действие можно представить как замену всех конструкторов в дереве значения на подходящие по типу функции. В этой маленькой функции кроется невероятная сила. Посмотрим на несколько примеров:
Prelude Data.Char> :m -Data.Char Prelude> let xs = [1,2,3,4,5] Prelude> foldr (:) [] xs [1,2,3,4,5]
Мы заменили конструкторы на самих себя и получили исходный список, теперь давайте сделаем что-нибудь более конструктивное. Например вычислим сумму всех элементов или произведение:
Prelude> foldr (+) 0 xs 15 Prelude> foldr (*) 1 xs 120 Prelude> foldr max (head xs) xs 5
В этой главе мы присмотрелись к типам и узнали как ограничения, общие для всех типов, сказываются на структуре значений. Мы узнали, что константы в Haskell очень похожи на деревья, а запись констант – на строчную запись дерева. Также мы присмотрелись к функциям и узнали, что операция определения синонима состоит из композиции и декомпозиции значений.
name декомпозиция = композиция
Существует несколько правил для построения композиций:
Одно для функций в префиксной форме записи:
f :: a -> b, x :: a
-------------------------------
(f x) :: bИ два для функций в инфиксной форме записи:
Это левое сечение:
(*) :: a -> (b -> c), x :: a
---------------------------------
(x *) :: b -> c
И правое сечение:
(*) :: a -> (b -> c), x :: b
---------------------------------
(* x) :: a -> cДекомпозиция происходит в аргументах функции. С её помощью мы можем извлечь из составной константы-дерева какую-нибудь часть или указать на какие константы мы реагируем в данном уравнении.
Ещё мы узнали о частичном применении. О том, что все функции в Haskell являются функциями одного аргумента, которые возвращают константы или другие функции одного аргумента.
Мы потренировались в составлении неправильных выражений и посмотрели как компилятор на основе правил применения узнаёт что они неправильные. Мы узнали, что такое ограничение мономорфизма и как оно появляется. Также мы присмотрелись к рекурсивным функциям.
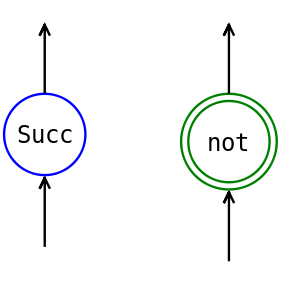
Конструкторы и синонимы
Составьте в интерпретаторе как можно больше неправильных выражений и посмотрите на сообщения об ошибках. Разберитесь почему выражение оказалось неправильным. Для этого проверьте типы с помощью правил применения. Составьте несколько выражений, ведущих к ошибке из-за ограничения мономорфизма.
Потренируйтесь в интерпретаторе с функциями map, filter и foldr. Попробуйте их с самыми разными функциями. Воспользуйтесь и теми функциями, что были определены в прошлой главе в тексте или в упражнениях.
В этой главе было много картинок и графических аналогий, попробуйте попрограммировать в картинках. Нарисуйте определённые нами функции или какие-нибудь новые в виде деревьев. Например, это можно сделать так. Мы будем отличать конструкторы от синонимов. Конструкторы будем рисовать в одинарном кружке, а синонимы в двойном.
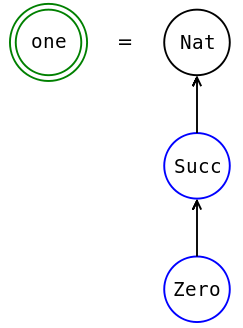
Синоним-константа
Мы будем все функции писать также как и прежде, но вместо аргументов слева от знака равно и выражений справа от знака равно, будем рисовать деревья.
Например, объявим простой синоним-константу. Мы будем дорисовывать сверху типы значений вместо объявления типа функции.
Несколько функций для списков. Извлечение первого элемента и функция преобразования всех элементов списка. Попробуйте в таком же духе определить несколько функций.
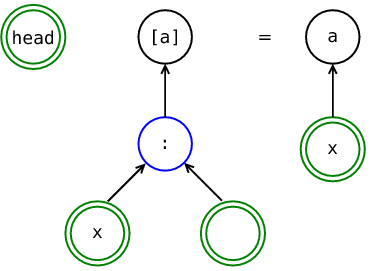
Функция извлечения первого элемента списка
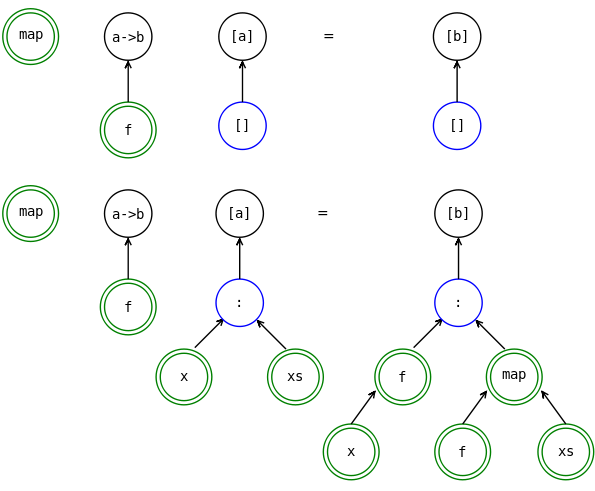
Функция преобразования элементов списка