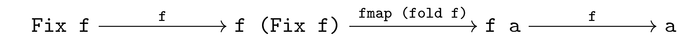
В этой главе мы узнаем как в теории категорий определяются типы. В теории категорий типы определяются как начальные и конечные объекты в специальных категориях, которые называются алгебрами функторов. Для понимания этой главы хорошо освежить в памяти главу о структурной рекурсии, там где мы говорили о свёртках и развёртках.
Оригами – состоит из двух слов “свёртка” и “бумага”. При программировании в стиле оригами все функции строятся через функции свёртки и развёртки. Есть даже такие языки программирования, в которых это единственный способ определения рекурсии. Этот стиль очень хорошо подходит для ленивых языков программирования, поскольку в связке:
fold f . unfold g
функции свёртки и развёртки работают синхронно. Функция развёртки не производит новых элементов до тех пор пока они не понадобятся во внешней функции свёртки.
Помните в одной из глав мы говорили о том, что рекурсивные функции можно определять через функцию fix.
Например так выглядит рекурсивная функция сложения всех чисел от одного до n:
sumInt :: Int -> Int sumInt 0 = 0 sumInt n = n + sumInt (n-1)
Эту функцию мы можем переписать с помощью функции fix. При вычислении fix f будет составлено значение
f (f (f (f ...)))
Теперь перепишем функцию sumInt через fix:
sumInt = fix $ \f n ->
case n of
0 -> 0
n -> n + f (n - 1)
Смотрите лямбда функция в аргументе fix принимает функцию и число, а возвращает число. Тип этой функции (Int -> Int) -> (Int -> Int). После применения функции fix мы как раз и получим функцию типа Int -> Int. В лямбда функции рекурсивный вызов был заменён на вызов функции-параметра f.
Оказывается, что этот приём может быть применён и для рекурсивных типов данных. Мы можем создать обобщённый тип, который обозначает рекурсивный тип:
newtype Fix f = Fix { unFix :: f (Fix f) }
В этой записи мы получаем уравнение неподвижной точки Fix f = f (Fix f), где f это некоторый тип с параметром. Определим тип целых чисел:
data N a = Zero | Succ a
deriving (Show, Eq)
type Nat = Fix N
Теперь создадим несколько конструкторов:
zero :: Nat zero = Fix Zero succ :: Nat -> Nat succ = Fix . Succ
Сохраним эти определения в модуле Fix.hs и посмотрим в интерпретаторе на значения и их типы, ghc не сможет вывести экземпляр Show для типа Fix, потому что он зависит от типа с параметром, а не от конкретного типа. Для решения этой проблемы нам придётся определить экземпляры вручную и подключить несколько расширений языка. Помните в главе о ленивых вычислениях мы подключали расширение BangPatterns? Нам понадобятся:
{-# Language FlexibleContexts, UndecidableInstances #-}
Теперь определим экземпляры для Show и Eq:
instance Show (f (Fix f)) => Show (Fix f) where
show x = "(" ++ show (unFix x) ++ ")"
instance Eq (f (Fix f)) => Eq (Fix f) where
a == b = unFix a == unFix b
Определим списки-оригами:
data L a b = Nil | Cons a b
deriving (Show, Eq)
type List a = Fix (L a)
nil :: List a
nil = Fix Nil
infixr 5 `cons`
cons :: a -> List a -> List a
cons a = Fix . Cons a
В типе L мы заменили рекурсивный тип на параметр. Затем в записи List a = Fix (L a) мы производим замыкание по параметру. Мы бесконечно вкладываем тип L a во второй параметр. Так получается рекурсивный тип для списков. Составим какой-нибудь список:
*Fix> :r [1 of 1] Compiling Fix ( Fix.hs, interpreted ) Ok, modules loaded: Fix. *Fix> 1 `cons` 2 `cons` 3 `cons` nil (Cons 1 (Cons 2 (Cons 3 (Nil))))
Спрашивается, зачем нам это нужно? Зачем нам записывать рекурсивные типы через тип Fix? Оказывается, при такой записи мы можем построить универсальные функции fold и unfold - они будут работать для любого рекурсивного типа.
Помните, как мы составляли функции свёртки? Мы строили воображаемый класс, в котором сворачиваемый тип заменялся на параметр. Например, для списка мы строили свёртку так:
class [a] b where
(:) :: a -> b -> b
[] :: b
После этого мы легко получали тип для функции свёртки:
foldr :: (a -> b -> b) -> b -> ([a] -> b)
Она принимает методы воображаемого класса, в котором тип записан с параметром, а возвращает функцию из рекурсивного типа в тип параметра.
Сейчас мы выполняем эту процедуру замены рекурсивного типа на параметр в обратном порядке. Сначала мы строим типы с параметром, а затем получаем из них рекурсивные типы с помощью конструкции Fix. Теперь методы класса с параметром это наши конструкторы исходных типов, а рекурсивный тип записан через Fix. Если мы сопоставим два способа, то мы сможем получить такой тип для функции свёртки:
fold :: (f b -> b) -> (Fix f -> b)
Смотрите, функция свёртки по-прежнему принимает методы воображаемого класса с параметром, но теперь класс перестал быть воображаемым, он стал типом с параметром. Результатом функции свёртки будет функция из рекурсивного типа Fix f в тип параметр.
Аналогично строится и функция unfold:
unfold :: (b -> f b) -> (b -> Fix f)
В первой функции мы указываем один шаг разворачивания рекурсивного типа, а функция развёртки рекурсивно распространяет этот один шаг на потенциально бесконечную последовательность применений этого одного шага.
Теперь давайте определим эти функции. Но для этого нам понадобится от типа f одно свойство - он должен быть функтором. Опираясь на это свойство, мы будем рекурсивно обходить этот тип.
fold :: Functor f => (f a -> a) -> (Fix f -> a) fold f = f . fmap (fold f) . unFix
Проверим эту функцию по типам. Для этого нарисуем схему композиции:
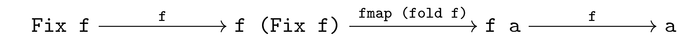
Сначала мы разворачиваем обёртку Fix и получаем значение типа f (Fix f), затем с помощью fmap мы внутри типа f рекурсивно вызываем функцию свёртки и в итоге получаем значение f a, на последнем шаге мы выполняем свёртку на текущем уровне вызовом функции f.
Аналогично определяется и функция unfold. Только теперь мы сначала развернём первый уровень, затем рекурсивно вызовем развёртку внутри типа f и только в самом конце завернём всё в тип Fix:
unfold :: Functor f => (a -> f a) -> (a -> Fix f) unfold f = Fix . fmap (unfold f) . f
Схема композиции:
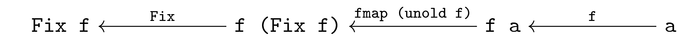
Возможно, вы уже догадались о том, что функция fold дуальна по отношению к функции unfold. Это особенно наглядно отражается на схеме композиции: при переходе от fold к unfold мы просто перевернули все стрелки и заменили разворачивание типа Fix на заворачивание в Fix.
Определим несколько функций для натуральных чисел и списков в стиле оригами. Для начала сделаем L и N экземпляром класса Functor:
instance Functor N where
fmap f x = case x of
Zero -> Zero
Succ a -> Succ (f a)
instance Functor (L a) where
fmap f x = case x of
Nil -> Nil
Cons a b -> Cons a (f b)
Это всё что нам нужно для того чтобы начать пользоваться функциями свёртки и развёртки! Определим экземпляр Num для натуральных чисел:
instance Num Nat where
(+) a = fold $ \x -> case x of
Zero -> a
Succ x -> succ x
(*) a = fold $ \x -> case x of
Zero -> zero
Succ x -> a + x
fromInteger = unfold $ \n -> case n of
0 -> Zero
n -> Succ (n-1)
abs = undefined
signum = undefined
Сложение и умножение определены через свёртку, а функция построения натурального числа из числа типа Integer определена через развёртку. Сравните с теми функциями, которые мы писали в главе про структурную рекурсию. Теперь мы не передаём отдельно две функции, на которые мы будем заменять конструкторы. Эти функции закодированы в типе с параметром. Для того, чтобы этот код заработал, нам придётся добавить ещё два расширения TypeSynonymInstances FlexibleInstances - наши рекурсивные типы являются синонимами, а не новыми типами. В рамках стандарта Haskell мы можем определять экземпляры только для новых типов и для того, чтобы обойти это ограничение, мы добавляем ещё два расширения.
*Fix> succ $ 1+2 (Succ (Succ (Succ (Succ (Zero))))) *Fix> ((2 * 3) + 1) :: Nat (Succ (Succ (Succ (Succ (Succ (Succ (Succ (Zero)))))))) *Fix> 2+2 == 2*(2::Nat) True
Определим функции на списках. Для начала зададим две вспомогательные функции, которые извлекают голову и хвост списка:
headL :: List a -> a
headL x = case unFix x of
Nil -> error "empty list"
Cons a _ -> a
tailL :: List a -> List a
tailL x = case unFix x of
Nil -> error "empty list"
Cons a b -> b
Теперь определим несколько новых функций:
mapL :: (a -> b) -> List a -> List b
mapL f = fold $ \x -> case x of
Nil -> nil
Cons a b -> f a `cons` b
takeL :: Int -> List a -> List a
takeL = curry $ unfold $ \(n, xs) ->
if n == 0 then Nil
else Cons (headL xs) (n-1, tailL xs)
appendL :: List a -> List a -> List a
appendL a b = fold (\x -> case x of
Nil -> b
Cons x' y' -> x' `cons` y') a
iterateL :: (a -> a) -> a -> List a
iterateL f = unfold $ \a -> Cons a $ f a
Сравните эти функции с теми, что мы определяли в главе о структурной рекурсии. Проверим, работают ли эти функции:
*Fix> :r [1 of 1] Compiling Fix ( Fix.hs, interpreted ) Ok, modules loaded: Fix. *Fix> takeL 3 $ iterateL (+1) zero (Cons (Zero) (Cons (Succ (Zero)) (Cons (Succ (Succ (Zero))) (Nil)))) *Fix> let x = 1 `cons` 2 `cons` 3 `cons` nil *Fix> mapL (+10) $ x `appendL` x (Cons 11 (Cons 12 (Cons 13 (Cons 11 (Cons 12 (Cons 13 (Nil)))))))
Обратите внимание на то, что с большими буквами мы пишем Cons и Nil, когда хотим закодировать функции для свёртки-развёртки, а с маленькой буквы пишем значения рекурсивного типа. Надеюсь, что вы разобрались на примерах как устроены функции fold и unfold, потому что теперь мы перейдём к теории, которая за этим стоит.
С точки зрения теории категорий функция свёртки является катаморфизмом, а функция развёртки – анаморфизмом. Напомню, что катаморфизм – это функция, которая ставит в соответствие объектам категории с начальным объектом стрелки, которые начинаются из начального объекта, а заканчиваются в данном объекте. Анаморфизм – это перевёрнутый наизнанку катаморфизм.
Начальным и конечным объектом будет рекурсивный тип. Вспомним тип свёртки:
fold :: Functor f => (f a -> a) -> (Fix f -> a)
Функция свёртки строит функции, которые ведут из рекурсивного типа в произвольный тип, поэтому в данном случае рекурсивный тип будет начальным объектом. Функция развёртки строит из произвольного типа данный рекурсивный тип: на языке теории категорий она строит стрелку из произвольного объекта в рекурсивный, а это означает, что рекурсивный тип будет конечным объектом.
unfold :: Functor f => (a -> f a) -> (a -> Fix f)
Категории, которые определяют рекурсивные типы таким образом, называются (ко)алгебрами функторов. Видите, в типе и той, и другой функции стоит требование о том, что f является функтором. Катаморфизм и анаморфизм отображают объекты в стрелки. По типу функций fold и unfold мы можем сделать вывод, что объектами в нашей категории для свёрток будут стрелки вида
f a -> a
или для развёрток:
a -> f a
А стрелками будут обычные функции одного аргумента. Теперь дадим более формальное определение.
Эндофунктор \(F : \mathcal{A}\rightarrow \mathcal{A}\) определяет стрелки \(\alpha : FA \rightarrow A\), которые называются \(F\)-алгебрами. Стрелку \(h : A \rightarrow B\) называют \(F\)-гомоморфизмом, если следующая диаграмма коммутирует:
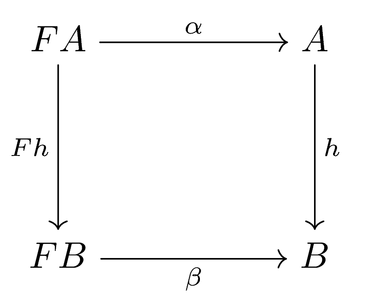
Или, можно сказать по-другому, для \(F\)-алгебр \(\alpha:FA \rightarrow A\) и \(\beta : FB \rightarrow B\) выполняется:
\[Fh \:\mathbf{;}\:\beta = \alpha \:\mathbf{;}\:h\]
Это свойство совпадает со свойством естественного преобразования – только вместо одного из функторов мы подставили тождественный функтор \(I\). Определим категорию \(\textbf{Alg}(F)\) для категории \(\mathcal{A}\) и эндофунктора \(F : \mathcal{A}\rightarrow \mathcal{A}\)
Объектами являются \(F\)-алгебры \(FA \rightarrow A\), где \(A\) – объект категории \(\mathcal{A}\)
Два объекта \(\alpha : FA \rightarrow A\) и \(\beta : FB \rightarrow B\) соединяет \(F\)-гомоморфизм \(h : A \rightarrow B\). Это такая стрелка из \(\mathcal{A}\), для которой выполняется:
\[Fh \:\mathbf{;}\:\beta = \alpha \:\mathbf{;}\:h\]
Если в этой категории есть начальный объект \(in_F : FT \rightarrow T\), то определён катаморфизм, который переводит объекты \(FA \rightarrow A\) в стрелки \(T \rightarrow A\). Причём следующая диаграмма коммутирует:

Этот катаморфизм и будет функцией свёртки для рекурсивного типа \(Т\). Понятие \(\textbf{Alg}(F)\) можно перевернуть и получить категорию \(\textbf{CoAlg}(F)\).
Объектами являются \(F\)-коалгебры \(A \rightarrow FA\), где \(A\) – объект категории \(\mathcal{A}\)
Два объекта \(\alpha : A \rightarrow FA\) и \(\beta : B \rightarrow FB\) соединяет \(F\)-когомоморфизм . Это такая стрелка из \(\mathcal{A}\), для которой выполняется:
\[h \:\mathbf{;}\:\alpha = \beta \:\mathbf{;}\:Fh\]
Композиция и тождественная стрелка взяты из категории \(\mathcal{A}\).
Если в этой категории есть конечный объект, то его называют \(out_F : T \rightarrow FT\). Тогда определён анаморфизм, который переводит объекты \(A \rightarrow FA\) в стрелки \(A \rightarrow T\).
Причём следующая диаграмма коммутирует:

Если для категории \(\mathcal{A}\) и функтора \(F\) определены стрелки \(in_F\) и \(out_F\), то они являются взаимнообратными и определяют изоморфизм \(T \cong FT\). Часто объект \(T\) в случае \(\textbf{Alg}(F)\) обозначают \(\mu_F\), поскольку начальный объект определяется функтором \(F\), а в случае \(\textbf{CoAlg}(F)\) обозначают \(\nu_F\).
Типы, которые являются начальными объектами, принято называть индуктивными, а типы, которые являются конечными объектами – коиндуктивными.
Мы говорили, что если начальный(конечный) объект существует, а когда он существует? Рассмотрим один важный случай. Если категория является категорией, в которой объектами являются полные частично упорядоченные множества, а стрелками являются монотонные функции, такие категории называют \(\textbf{CPO}\), и функтор – полиномиальный, то начальный и конечный объекты существуют.
Оказывается на значениях можно ввести частичный порядок. Порядок называется частичным, если отношение \(\leq\) определено не для всех элементов, а лишь для некоторых из них. Частичный порядок на значениях отражает степень неопределённости значения. Самый маленький объект это полностью неопределённое значение \(\bot\). Любое значение типа содержит больше определённости чем \(\bot\).
Для того чтобы не путать упорядочивание значений по степени определённости с обычным числовым порядком, пользуются специальным символом \(\sqsubseteq\). Запись
\[a \sqsubseteq b\]
означает, что \(b\) более определено (или информативнее) чем \(a\).
Так для логических значений определены два нетривиальных сравнения:
\[data\ Bool\ =\ True \ |\ False\]
\[\bot \sqsubseteq True\] \[\bot \sqsubseteq False\]
Мы будем называть нетривиальными сравнения в которых, компоненты слева и справа от \(\sqsubseteq\) не равны. Например ясно, что \(True \sqsubseteq True\) или \(\bot \sqsubseteq \bot\). Это тривиальные сравнения и мы их будем лишь подразумевать. Считается, что если два значения определены полностью, то мы не можем сказать какое из них информативнее. Так к примеру для логических значений мы не можем сказать какое значение более определено \(True\) или \(False\).
Рассмотрим пример по-сложнее. Частично определённые значения:
\[data\ Maybe\ a = Nothing \ |\ Just\ a\]
| \(\bot\) | \(\sqsubseteq\) | \(Nothing\) |
| \(\bot\) | \(\sqsubseteq\) | \(Just\ \bot\) |
| \(\bot\) | \(\sqsubseteq\) | \(Just\ a\) |
| \(Just\ a\) | \(\sqsubseteq\) | \(Just\ b\), если \(a \sqsubseteq b\) |
Если вспомнить как происходит вычисление значения, то значение \(a\) менее определено чем \(b\), если взрывное значение \(\bot\) в \(a\) находится ближе к корню значения, чем в \(b\). Итак получается, что в категории \(\textbf{Hask}\) объекты это множества с частичным порядком. Что означает требование монотонности функции?
Монотонность в контексте операции \(\sqsubseteq\) говорит о том, что чем больше определён вход функции тем больше определён выход:
\[a \sqsubseteq b \quad \Rightarrow \quad f\ a \sqsubseteq f\ b\]
Это требование накладывает запрет на возможность проведения сопоставления с образцом по значению \(\bot\). Иначе мы можем определять немонотонные функции вроде:
isBot :: Bool -> Bool isBot undefined = True isBot _ = undefined
Полнота частично упорядоченного множества означает, что у любой последовательности \(x_n\)
\[x_0 \sqsubseteq x_1 \sqsubseteq x_2 \sqsubseteq ...\]
есть значение \(x\), к которому она сходится. Это значение называют супремумом множества. Что такое полные частично упорядоченные множества мы разобрались. А что такое полиномиальный функтор?
Полиномиальный функтор – это функтор который построен лишь с помощью операций суммы, произведения, постоянных функторов, тождественного фуктора и композиции функторов. Определим эти операции:
Сумма функторов \(F\) и \(G\) определяется через операцию суммы объектов:
\[(F+G)X = FX + GX\]
Произведение функторов \(F\) и \(G\) определяется через операцию произведения объектов:
\[(F\times G)X = FX \times GX\]
Постоянный функтор отображает все объекты категории в один объект, а стрелки в тождественную стрелку этого объекта, мы будем обозначать постоянный функтор подчёркиванием:
| \(\underline{A}X\) | \(=\) | \(A\) |
| \(\underline{A}f\) | \(=\) | \(id_A\) |
Тождественный функтор оставляет объекты и стрелки неизменными:
| \(IX\) | \(=\) | \(X\) |
| \(If\) | \(=\) | \(f\) |
Композиция функторов \(F\) и \(G\) это последовательное применение функторов
\[FGX = F(GX)\]
По определению функции построенные с помощью этих операций называют полиномиальными. Определим несколько типов данных с помощью полиномиальных функторов. Определим логические значения:
\[Bool = \mu(\underline{1} + \underline{1})\]
Объект \(1\) обозначает любую константу, это конечный объект исходной категории. Нам не важны имена конструкторов, но важна структура типа. \(\mu\) обозначает начальный объект в \(F\)-алгебре.
Определим натуральные числа:
\[Nat = \mu(\underline{1} + I)\]
Эта запись обозначает начальный объект для \(F\)-алгебры с функтором \(F=\underline{1}+I\). Посмотрим на определение списка:
\[List_A = \mu(\underline{1} + \underline{A} \times I)\]
Список это начальный объект \(F\)-алгебры \(\underline{1}+\underline{A}\times I\). Также можно определить бинарные деревья:
\[BTree_A = \mu(\underline{A} + I \times I )\]
Определим потоки:
\[Stream_A = \nu (\underline{A} \times I)\]
Потоки являются конечным объектом \(F\)-коалгебры, где \(F= \underline{A} \times I\).
Оказывается, что с помощью катаморфизма и анаморфизма мы можем определить функцию fix, то есть мы можем выразить любую рекурсивную функцию с помощью структурной рекурсии.
Функция fix строит бесконечную последовательность применений некоторой функции f.
f (f (f ...)))
Сначала с помощью анаморфизма мы построим бесконечный список, который содержит функцию f во всех элементах:
repeat f = f : f : f : ...
А затем заменим конструктор : на применение. В итоге мы получим такую функцию:
fix :: (a -> a) -> a fix = foldr ($) undefined . repeat
Убедимся, что эта функция работает:
Prelude> let fix = foldr ($) undefined . repeat Prelude> take 3 $ fix (1:) [1,1,1] Prelude> fix (\f n -> if n==0 then 0 else n + f (n-1)) 10 55
Теперь давайте определим функцию fix через функции cata и ana:
cata :: Functor f => (f a -> a) -> Fix f -> a cata = fold ana :: Functor f => (a -> f a) -> a -> Fix f ana = unfold fix :: (a -> a) -> a fix = cata (\(Cons f a) -> f a) . ana (\a -> Cons a a)
Эта связка анаморфизм с последующим катаморфизмом встречается так часто, что ей дали специальное имя. Гиломорфизмом называют функцию:
hylo :: Functor f => (f b -> b) -> (a -> f a) -> (a -> b) hylo phi psi = cata phi . ana psi
Отметим, что эту функцию можно выразить и по-другому:
hylo :: Functor f => (f b -> b) -> (a -> f a) -> (a -> b) hylo phi psi = phi . (fmap $ hylo phi psi) . psi
Этот вариант более эффективен по расходу памяти: мы не строим промежуточное значение Fix f, а сразу обрабатываем значения в функции phi по ходу их построения в функции psi. Давайте введём инфиксную операцию гиломорфизм для этого определения:
(>>) :: Functor f => (a -> f a) -> (f b -> b) -> (a -> b) psi >> phi = phi . (fmap $ hylo phi psi) . psi
Теперь давайте скроем одноимённую функцию из Prelude и определим несколько рекурсивных функций с помощью гиломорфизма. Начнём с функции вычисления суммы чисел от нуля до данного числа:
sumInt :: Int -> Int
sumInt = range >> sum
sum x = case x of
Nil -> 0
Cons a b -> a + b
range n
| n == 0 = Nil
| otherwise = Cons n (n-1)
Сначала мы создаём в функции range список всех чисел от данного числа до нуля, а затем в функции sum складываем значения. Теперь мы можем легко определить функцию вычисления факториала:
fact :: Int -> Int
fact = range >> prod
prod x = case x of
Nil -> 1
Cons a b -> a * b
Напишем функцию, которая извлекает из потока n-тый элемент. Сначала определим тип для потока:
type Stream a = Fix (S a)
data S a b = a :& b
deriving (Show, Eq)
instance Functor (S a) where
fmap f (a :& b) = a :& f b
headS :: Stream a -> a
headS x = case unFix x of
(a :& _) -> a
tailS :: Stream a -> Stream a
tailS x = case unFix x of
(_ :& b) -> b
Теперь функцию извлечения элемента:
getElem :: Int -> Stream a -> a
getElem = curry (enum >> elem)
where elem ((n, a) :& next)
| n == 0 = a
| otherwise = next
enum (a, st) = (a, headS st) :& (a-1, tailS st)
В функции enum мы добавляем к элементам потока убывающую последовательность чисел, она стартует из данного числа. Элемент, который нам нужен, будет содержать в этой последовательности число ноль. В функции elem мы как раз и извлекаем тот элемент, рядом с которым хранится число ноль. Обратите внимание на то, что рекурсия встроена в этот алгоритм: если данное число не равно нулю, мы просто извлекаем следующий элемент.
С помощью этой функции мы можем вычислить n-тое число из ряда чисел Фибоначчи. Сначала создадим поток чисел Фибоначчи:
fibs :: Stream Int fibs = ana (\(a, b) -> a :& (b, a+b)) (0, 1)
Теперь просто извлечём n-тый элемент из потока чисел Фибоначчи:
fib :: Int -> Int fib = flip getElem fibs
Вычислим поток всех простых чисел. Мы будем вычислять его по алгоритму “решето Эратосфена”. В начале алгоритма у нас есть поток целых чисел и известно, что первое число является простым.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 …
В процессе этого алгоритма мы вычёркиваем все не простые числа. Сначала мы ищем первое незачёркнутое число и помещаем его в результирующий поток, а на следующий шаг алгоритма мы передаём исходный поток, в котором зачёркнуты все числа кратные тому, что мы положили последним:
2
3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …
Теперь мы ищем первое незачёркнутое число и помещаем его в результат. А на следующий шаг рекурсии передаём поток, в котором зачёркнуты все числа кратные новому простому числу:
2, 3
4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, …
И так далее. На каждом шаге мы будем получать одно простое число. Зачёркивание мы будем имитировать с помощью типа Maybe. Всё начинается с потока целых чисел, в котором не зачёркнуто ни одно число:
nums :: Stream (Maybe Int) nums = mapS Just $ iterateS (+1) 2 mapS :: (a -> b) -> Stream a -> Stream b mapS f = ana $ \xs -> (f $ headS xs) :& tailS xs iterateS :: (a -> a) -> a -> Stream a iterateS f = ana $ \x -> x :& f x
В силу ограничений системы типов Haskell мы не можем определить экземпляр Functor для типа Stream, поскольку Stream является не самостоятельным типом, а типом-синонимом. Поэтому нам приходится определить функцию mapS. Определим шаг рекурсии:
primes :: Stream Int
primes = ana erato nums
erato xs = n :& dropWhileS isNothing (erase n xs)
where n = fromJust $ headS xs
Переменная n содержит первое незачёркнутое число на данном шаге. Функции isNothing и fromJust взяты из стандартного модуля Data.Maybe. Нам осталось определить лишь две функции. Это аналог функции dropWhile на списках: она удаляет из начала списка все элементы, которые удовлетворяют некоторому предикату. Вторая функция erase вычёркивает все числа в потоке кратные данному.
dropWhileS :: (a -> Bool) -> Stream a -> Stream a
dropWhileS p = psi >> phi
where phi ((b, xs) :& next) = if b then next else xs
psi xs = (p $ headS xs, xs) :& tailS xs
В этой функции мы сначала генерируем список пар, который содержит значения предиката и остатки списка, а затем находим в этом списке первый такой элемент, значение которого равно False.
erase :: Int -> Stream (Maybe a) -> Stream (Maybe a)
erase n xs = ana phi (0, xs)
where phi (a, xs)
| a == 0 = Nothing :& (a', tailS xs)
| otherwise = headS xs :& (a', tailS xs)
where a' = if a == n-1 then 0 else (a+1)
В функции erase мы заменяем на Nothing каждый элемент, порядок следования которого кратен аргументу n. Проверим, что у нас получилось:
*Fix> primes (2 :& (3 :& (5 :& (7 :& (11 :& (13 :& (17 :& (19 :& (23 :& (29 :& (31 :& (37 :& (41 :& (43 :& (47 :& (53 :& (59 :& (61 :& (67 :& (71 :& (73 :& (79 :& (83 :& (89 :& (97 :& (101 :& (103 :& (107 :& (109 :& (113 :& (127 :& (131 :& ...
В этой главе мы узнали, что любая рекурсивная функция может быть выражена через структурную рекурсию. Мы узнали как в теории категорий определяются типы. Типы являются начальными и конечными объектами в специальных категориях, которые называются алгебрами функторов. Слоган теории категорий гласит:
Управляющие структуры определяются структурой типов.
Определив тип, мы получаем вместе с ним две функции структурной рекурсии, это катаморфизм (для начальных объектов) и анаморфизм (для конечных объектов). С помощью катаморфизма мы можем сворачивать значение данного типа в значения любого другого типа, а с помощью анаморфизма мы можем разворачивать значения данного типа из значений любого другого типа. Также мы узнали, что категория \(\textbf{Hask}\) является категорией \(\textbf{CPO}\), категорией полных частично упорядоченных множеств.
Потренируйтесь в определении рекурсивных функций через гиломорфизм. Попробуйте переписать как можно больше определений из главы о структурной рекурсии в терминах типа Fix и функций cata, ana и hylo. Также потренируйтесь на стандартных функциях из модуля Prelude. Определите новые типы через Fix, например, деревья из модуля Data.Tree. Попробуйте свои силы на функциях по-сложнее, например, алгоритме эвристического поиска.
Определите монадные версии рекурсивных функций:
cataM :: (Monad m, Traversable t) => (t a -> m a) -> Fix t -> m a anaM :: (Monad m, Traversable t) => (a -> m (t a)) -> (a -> m (Fix t)) hyloM :: (Monad m, Traversable t) => (t b -> m b) -> (a -> m (t a)) -> (a -> m b)
С помощью этих функций мы, например, можем преобразовывать дерево выражения и при этом обновлять какое-нибудь состояние или читать из общего окружения.
В этом определении стоит новый класс Traversable. Разберитесь с ним самостоятельно. Немного подскажу. Этот класс появился вместе с классом Applicative. Когда разработчики поняли о существовании полезной абстракции, которая ослабляет класс Monad, они также обратили внимание на функцию sequence:
sequence :: Monad m => [m a] -> m [a] sequence = foldr (liftM2 (:)) (return [])
Эту функцию можно записать с помощью одних лишь методов класса Applicative. Поэтому ограничение в контексте функции избыточно. Класс Traversable предназначени для устранения этой неточности. Посмотрим на основной метод класса:
class (Functor t, Foldable t) => Traversable t where
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
Тип очень похож на тип функции mapM. И не случайно, ведь mapM определяется через sequence. Только теперь вместо списка стоит более общий тип. Это тип Foldable, который определяет список как нечто, на чём можно проводить операции свёртки.