
Многие понятия в Haskell позаимствованы из теории категорий, например это функторы, монады. Теория категорий – это скорее язык, математический жаргон, она настолько общая, что кажется ей нет никакого применения. Возможно это и так, но в этом языке многие сущности, которые лишь казались родственными и было смутное интуитивное ощущение их близости, становятся тождественными.
Теория категорий занимается описанием функций. В лямбда-исчислении основной операцией была подстановка значения в функцию, а в теории категорий мы сосредоточимся на операции композиции. Мы будем соединять различные объекты так, чтобы структура объектов сохранялась. Структура объекта будет определяться свойствами, которые продолжают выполнятся после преобразования объекта.
Мы будем говорить об объектах и связях между ними. Связи принято называть “стрелками” или “морфизмами”. Далее мы будем пользоваться термином стрелка. У стрелки есть начальный объект, его называют доменом (domain) и конечный объект, его называют кодоменом (codomain).

В этой записи стрелка \(f\) соединяет объекты \(A\) и \(B\), в тексте мы будем писать это так \(f:A \rightarrow B\), словно стрелка это функция, а объекты это типы. Мы будем обозначать объекты большими буквами \(A\), \(B\), \(C\), …, а стрелки – маленькими буквами \(f\), \(g\), \(h\), … Для того чтобы связи было интереснее изучать мы введём такое правило:

Если конец стрелки \(f\) указывает на начало стрелки \(g\), то должна быть такая стрелка \(f \:\mathbf{;}\:g\), которая обозначает составную стрелку. Вводится специальная операция “точка с запятой”, которая называется композицией стрелок: Это правило говорит о том, что связи распространяются по объектам. Теперь у нас есть не просто объекты и стрелки, а целая сеть объектов, связанных между собой. Тот факт, что связи действительно распространяются отражается свойством:
\[f \:\mathbf{;}\:(g \:\mathbf{;}\:h) = (f \:\mathbf{;}\:g) \:\mathbf{;}\:h\]
Это свойство называют ассоциативностью. Оно говорит о том, что стрелки, которые образуют составную стрелку являются цепочкой и нам не важен порядок их группировки, важно лишь кто за кем идёт. Подразумевается, что стрелки \(f\), \(g\) и \(h\) имеют подходящие типы для композиции, что их можно соединять. Это свойство похоже на интуитивное понятие пути, как цепочки отрезков.
Связи между объектами можно трактовать как преобразования объектов. Стрелка \(f : A \rightarrow B\) – это способ, с помощью которого мы можем перевести объект \(A\) в объект \(B\). Композиция в этой аналогии приобретает естественную интерпретацию. Если у нас есть способ \(f : A \rightarrow B\) преобразования объекта \(A\) в объект \(B\), и способ \(g : B \rightarrow C\) преобразования объекта \(B\) в объект \(C\), то мы конечно можем, применив сначала \(f\), а затем \(g\), получить из объекта \(A\) объект \(C\).
Когда мы думаем о стрелках как о преобразовании, то естественно предположить, что у нас есть преобразование, которое ничего не делает, как тождественная функция. В будем говорить, что для каждого объекта \(A\) есть стрелка \(id_A\), которая начинается из этого объекта и заканчивается в нём же.
\[id_A : A \rightarrow A\]
Тот факт, что стрелка \(id_A\) ничего не делает отражается свойствами, которые должны выполняться для всех стрелок:
| \(id_A \:\mathbf{;}\:f\) | \(=\) | \(f\) |
| \(f \:\mathbf{;}\:id_A\) | \(=\) | \(f\) |
Если мы добавим к любой стрелке тождественную стрелку, то от этого ничего не изменится.
Всё готово для того чтобы дать формальное определение понятия категории (category). Категория это:
Набор объектов (object).
Набор стрелок (arrow) или морфизмов (morphism).
Каждая стрелка соединяет два объекта, но объекты могут совпадать. Так обозначают, что стрелка \(f\) начинается в объекте \(A\) и заканчивается в объекте \(B\):
\[f : A \rightarrow B\]
При этом стрелка соединяет только два объекта:
\[f : A \rightarrow B,\ f : A' \rightarrow B' \qquad \Rightarrow \qquad A=A',\ B=B'\]
Определена операция композиции или соединения стрелок. Если конец одной стрелки совпадает с началом другой, то их можно соединить вместе:
\[f:A \rightarrow B,\ g : B\rightarrow C \quad \Rightarrow \quad f \:\mathbf{;}\:g : A \rightarrow C\]
Для каждого объекта есть стрелка, которая начинается и заканчивается в этом объекте. Эту стрелку называют тождественной (identity):
\[id_A : A \rightarrow A\]
Должны выполняться аксиомы:
Тождество \(id\)
\[id \:\mathbf{;}\:f = f\]
\[f \:\mathbf{;}\:id = f\]
Ассоциативность \(\:\mathbf{;}\:\)
\[f \:\mathbf{;}\:(g \:\mathbf{;}\:h) = (f \:\mathbf{;}\:g) \:\mathbf{;}\:h\]
Приведём примеры категорий.
Одна точка с одной тождественной стрелкой образуют категорию.
В категории Set объектами являются все множества, а стрелками – функции. Стрелки соединяются с помощью композиции функций, тождественная стрелка, это тождественная функция.
В категории Hask объектами являются типы Haskell, а стрелками – функции, стрелки соединяются с помощью композиции функций, тождественная стрелка, это тождественная функция.
Ориентированный граф может определять категорию. Объекты – это вершины, а стрелки это связанные пути в графе. Соединение стрелок – это соединение путей, а тождественная стрелка, это путь в котором нет ни одного ребра.
Упорядоченное множество, в котором есть операция сравнения на больше либо равно задаёт категорию. Объекты – это объекты множества. А стрелки это пары объектов таких, что первый объект меньше второго. Первый объект в паре считается начальным, а второй конечным.
\[(a, b) : a \rightarrow b \qquad \text{если } a \leq b\]
Стрелки соединяются так:
\[(a, b) \:\mathbf{;}\:(b, c) = (a, c)\]
Тождественная стрелка состоит из двух одинаковых объектов:
\[id_a = (a, a)\]
Можно убедиться в том, что это действительно категория. Для этого необходимо проверить аксиомы ассоциативности и тождества. Важно проверить, что те стрелки, которые получаются в результате композиции, не нарушали бы основного свойства данной структуры, то есть тот факт, что второй элемент пары всегда больше либо равен первого элемента пары.
Отметим, что бывают такие области, в которых стрелки или преобразования с одинаковыми именами могут соединять несколько разных объектов. Например в Haskell есть классы, поэтому функции с одними и теми же именами могут соединять разные объекты. Если все условия категории для объектов и стрелок выполнены, кроме этого, то такую систему называют прекатегорией (pre-category). Из любой прекатегории не сложно сделать категорию, если включить имена объектов в имя стрелки. Тогда у каждой стрелки будут только одна пара объектов, которые она соединяет.
Вспомним определение класса Functor:
class Functor f where
fmap :: (a -> b) -> (f a -> f b)
В этом определении участвуют тип f и метод fmap. Можно сказать, что тип f переводит произвольные типы a в специальные типы f a. В этом смысле тип f является функцией, которая определена на типах. Метод fmap переводит функции общего типа a -> b в специальные функции f a -> f b.
При этом должны выполняться свойства:
fmap id = id fmap (f . g) = fmap f . fmap g
Теперь вспомним о категории Hask. В этой категории объектами являются типы, а стрелками функции. Функтор f отображает объекты и стрелки категории Hask в объекты и стрелки f Hask. При этом оказывается, что за счёт свойств функтора f Hask образует категорию.
Объекты – это типы f a.
Стрелки – это функции fmap f.
Композиция стрелок это просто композиция функций.
Тождественная стрелка это fmap id.
Проверим аксиомы:
fmap f . fmap id = fmap f . id = fmap f
fmap id . fmap f = id . fmap f = fmap f
fmap f . (fmap g . fmap h)
= fmap f . fmap (g . h)
= fmap (f . (g . h))
= fmap ((f . g) . h)
= fmap (f . g) . fmap h
= (fmap f . fmap g) . fmap h
Видно, что аксиомы выполнены, так функтор f порождает категорию f Hask. Интересно, что поскольку Hask содержит все типы, то она содержит и типы f Hask. Получается, что мы построили категорию внутри категории. Это можно пояснить на примере списков. Тип [] погружает любой тип в список, а функцию для любого типа можно превратить в функцию, которая работает на списках с помощью метода fmap. При этом с помощью класса Functor мы проецируем все типы и все функции в мир списков [a]. Но сам этот мир списков содержится в категории Hask.
С помощью функторов мы строим внутри одной категории другую категорию, при этом внутренняя категория обладает некоторой структурой. Так если раньше у нас были только произвольные типы a и произвольные функции a -> b, то теперь все объекты имеют тип [a] и все функции имеют тип [a] -> [b]. Также и функтор Maybe переводит произвольное значение, в значение, которое обладает определённой структурой. В нём выделен дополнительный элемент Nothing, который обозначает отсутствие значения. Если по типу val :: a мы ничего не можем сказать о содержании значения val, то по типу val :: Maybe a, мы знаем один уровень конструкторов. Например мы уже можем проводить сопоставление с образцом.
Теперь давайте вернёмся к теории категорий и дадим формальное определение понятия. Пусть \(\mathcal{A}\) и \(\mathcal{B}\) – категории, тогда функтором из \(\mathcal{A}\) в \(\mathcal{B}\) называют отображение \(F\), которое переводит объекты \(\mathcal{A}\) в объекты \(\mathcal{B}\) и стрелки \(\mathcal{A}\) в стрелки \(\mathcal{B}\), так что выполнены следующие свойства:
| \(F f\) | \(:\) | \(FA \rightarrow _{\mathcal{B}} FB\) | если \(f: A \rightarrow _{\mathcal{A}} B\) |
| \(F id_A\) | \(=\) | \(id_{FA}\) | для любого объекта |
| \(A\) из \(\mathcal{A}\) | |||
| \(F (f \:\mathbf{;}\:g)\) | \(=\) | \(Ff \:\mathbf{;}\:Fg\) | если \((f \:\mathbf{;}\:g)\) |
Здесь запись \(\rightarrow _\mathcal{A}\) и \(\rightarrow _\mathcal{B}\) означает, что эти стрелки в разных категориях. После отображения стрелки \(f\) из категории \(\mathcal{A}\) мы получаем стрелку в категории \(\mathcal{B}\), это и отражено в типе \(Ff : FA \rightarrow _\mathcal{B}FB\). Первое свойство говорит о том, что после отображения стрелки соединяют те же объекты, что и до отображения. Второе свойства говорит о сохранении тождественных стрелок. А последнее свойство, говорит о том, что “пути” между объектами также сохраняются. Если мы находимся в категории \(\mathcal{A}\) в объекте \(A\) и перед нами есть путь состоящий из нескольких стрелок в объект \(B\), то неважно как мы пойдём в \(FB\) либо мы пройдём этот путь в категории \(\mathcal{A}\) и в самом конце переместимся в \(FB\) или мы сначала переместимся в \(FA\) и затем пройдём по образу пути в категории \(FB\). Так и так мы попадём в одно и то же место. Схематически это можно изобразить так:

Стрелки сверху находятся в категории \(\mathcal{A}\), а стрелки снизу находятся в категории \(\mathcal{B}\). Функтор \(F : \mathcal{A}\rightarrow \mathcal{A}\), который переводит категорию \(\mathcal{A}\) в себя называют эндофунктором (endofunctor). Функторы отображают одни категории в другие сохраняя структуру первой категории. Мы словно говорим, что внутри второй категории есть структура подобная первой. Интересно, что последовательное применение функторов, также является функтором. Мы будем писать последовательное применение функторов \(F\) и \(G\) слитно, как \(FG\). Также можно определить и тождественный функтор, который ничего не делает с категорией, мы будем обозначать его как \(I_\mathcal{A}\) или просто \(I\), если категория на которой он определён понятна из контекста. Это говорит о том, что мы можем построить категорию, в которой объектами будут другие категории, а стрелками будут функторы.
В программировании часто приходится переводить данные из одной структуры в другую. Каждая из структур хранит какие-то конкретные значения, но мы ничего с ними не делаем мы просто перекладываем содержимое из одного ящика в другой. Например в нашем ящике только один отсек, но вдруг нам пришло бесконечно много подарков, что поделать нам приходится сохранить первый попавшийся, отбросив остальные. Главное в этой аналогии это то, что мы ничего не меняем, а лишь перекладываем содержимое из одной структуры в другую.
В Haskell это можно описать так:
onlyOne :: [a] -> Maybe a onlyOne [] = Nothing onlyOne (a:as) = Just a
В этой функции мы перекладываем элементы из списка [a] в частично определённое значение Maybe. Тоже самое происходит и в функции concat:
concat :: [[a]] -> [a]
Элементы перекладываются из списка списков в один список. В теории категорий этот процесс называется естественным преобразованием. Структуры определяются функторами. Поэтому в определении будет участвовать два функтора. В функции onlyOne это были функторы [] и Maybe. При перекладывании элементов мы можем просто выбросить все элементы:
burnThemALl :: [a] -> () burnThemAll = const ()
Можно сказать, что единичный тип также определяет функтор. Это константный функтор, он переводит любой тип в единственное значение (), а функцию в id:
data Empty a = Empty
instance Functor Empty where
fmap = const id
Тогда тип функции burnThemAll будет параметризован и слева и справа от стрелки:
burnThemAll :: [a] -> Empty a burnThemAll = const Empty
Пусть даны две категории \(\mathcal{A}\) и \(\mathcal{B}\) и два функтора \(F,G : \mathcal{A}\rightarrow \mathcal{B}\). Преобразованием (transformation) в \(\mathcal{B}\) из \(F\) в \(G\) называют семейство стрелок \(\varepsilon\):
\[\varepsilon_A : FA \rightarrow _\mathcal{B}GA \qquad \text{для любого } A \text{ из } \mathcal{A}\]
Рассмотрим преобразование onlyOne :: [a] -> Maybe a. Категории \(\mathcal{A}\) и \(\mathcal{B}\) в данном случае совпадают~– это категория Hask. Функтор \(F\) – это список, а функтор \(G\) это Maybe. Преобразование onlyOne для каждого объекта a из Hask определяет стрелку
onlyOne :: [a] -> Maybe a
Так мы получаем семейство стрелок, параметризованное объектом из Hask:
onlyOne :: [Int] -> Maybe Int onlyOne :: [Char] -> Maybe Char onlyOne :: [Int -> Int] -> Maybe (Int -> Int) ... ...
Теперь давайте определим, что значит перекладывать из одной структуры в другую, не меняя содержания. Представим, что функтор – это контейнер. Мы можем менять его содержание с помощью метода fmap. Например мы можем прибавить единицу ко всем элементам списка xs с помощью выражения . Точно так же мы можем прибавить единицу к частично определённому значению. С точки зрения теории категорий суть понятия “останется неизменным при перекладывании” заключается в том, что если мы возьмём любую функцию к примеру прибавление единицы, то нам неважно когда её применять до функции onlyOne или после. И в том и в другом случае мы получим одинаковый ответ. Давайте убедимся в этом:
onlyOne $ fmap (+1) [1,2,3,4,5]
=> onlyOne [2,3,4,5,6]
=> Just 2
fmap (+1) $ onlyOne [1,2,3,4,5]
=> fmap (+1) $ Just 1
=> Just 2
Результаты сошлись, обратите внимание на то, что функции fmap (+1) в двух вариантах являются разными функциями. Первая работает на списках, а вторая на частично определённых значениях. Суть в том, что если при перекладывании значение не изменилось, то нам не важно когда выполнять преобразование внутри функтора [] или внутри функтора Maybe. Теперь давайте выразим это на языке теории категорий.
Преобразование \(\varepsilon\) в категории \(\mathcal{B}\) из функтора \(F\) в функтор \(G\) называют естественным (natural), если
\[Ff \:\mathbf{;}\:\varepsilon_B \ =\ \varepsilon_A \:\mathbf{;}\:Gf \qquad \text{для любого } f : A \rightarrow _\mathcal{A}B\]
Это свойство можно изобразить графически:

По смыслу ясно, что если у нас есть три структуры данных (или три функтора), и мы просто переложили данные из первой во вторую, а затем переложили данные из второй в третью, ничего не меняя, то итоговое преобразование, которое составлено из последовательного применения перекладывания данных, также не меняет данные. Это говорит о том, что композиция двух естественных преобразований также является естественным преобразованием. Также мы можем составить тождественное преобразование: для двух одинаковых функторов \(F : \mathcal{A}\rightarrow \mathcal{B}\), это будет семейство тождественных стрелок в . Получается, что для двух категорий \(\mathcal{A}\) и \(\mathcal{B}\) мы можем составить категорию \(Ftr(\mathcal{A},\mathcal{B})\), в которой объектами будут функторы из \(\mathcal{A}\) в \(\mathcal{B}\), а стрелками будут естественные преобразования. Поскольку естественные преобразования являются стрелками, которые соединяют функторы, мы будем обозначать их как обычные стрелки. Так запись \(\eta : F \rightarrow G\) обозначает преобразование \(\eta\), которое переводит функтор \(F\) в функтор \(G\).
Интересно, что изначально создатели теории категорий Саундедерс Маклейн и Сэмюэль Эйленберг придумали понятие естественного преобразования, а затем, чтобы дать ему обоснование было придумано понятие функтора, и наконец для того чтобы дать обоснование функторам были придуманы категории. Категории содержат объекты и стрелки, для стрелок есть операция композиции. Также для каждого объекта есть тождественная стрелка. Функторы являются стрелками в категории, в которой объектами являются другие категории. А естественные преобразования являются стрелками в категории, в которой объектами являются функторы. Получается такая иерархия структур.
Монадой называют эндофунктор \(T:\mathcal{A}\rightarrow \mathcal{A}\), для которого определены два естественных преобразования \(\eta : I \rightarrow T\) и \(\mu : TT \rightarrow T\) и выполнены два свойства:
\(T \eta_A \:\mathbf{;}\:\mu_{A} \ =\ id_{TA}\)
\(T \mu_A \:\mathbf{;}\:\mu_{A} = \mu_{TA} \:\mathbf{;}\:\mu_A\)
Преобразование \(\eta\) – это функция return, а преобразование \(\mu\) – это функция join. В теории категорий в классе Monad другие методы. Перепишем эти свойства в виде функций Haskell:
join . fmap return = id join . fmap join = join . join
Порядок следования аргументов изменился, потому что мы пользуемся обычной композицией (через точку). Выражение \(T \eta_A\) означает применение функтора \(T\) к стрелке \(\eta_A\). Ведь преобразование это семейство стрелок, которые параметризованы объектами категории. На языке Haskell это означает применить fmap к полиморфной функции (функции с параметром).
Также эти свойства можно изобразить графически:
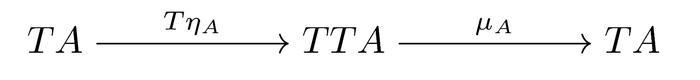
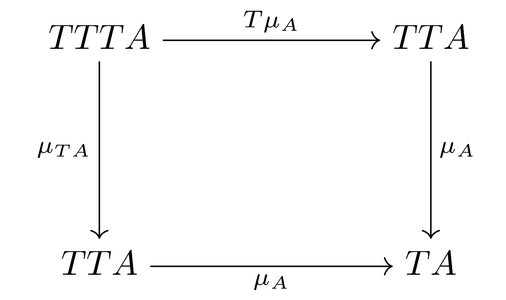
Если у нас есть монада \(T\), определённая в категории \(\mathcal{A}\), то мы можем построить в этой категории категорию специальных стрелок вида \(A \rightarrow TB\). Эту категорию называют категорией Клейсли.
Объекты категории Клейсли \(\mathcal{A}_T\) – это объекты исходной категории \(\mathcal{A}\).
Стрелки в \(\mathcal{A}_T\) это стрелки из \(\mathcal{A}\) вида \(A \rightarrow TB\), мы будем обозначать их \(A \rightarrow _T B\)
Композиция стрелок \(f : A \rightarrow _T B\) и \(g : B \rightarrow _T C\) определена с помощью естественных преобразований монады \(T\):
\[f \:\mathbf{;_{T}}\:g = f \:\mathbf{;}\:Tg \:\mathbf{;}\:\mu\]
Значок \(\:\mathbf{;_{T}}\:\) указывает на то, что слева от равно композиция в \(\mathcal{A}_T\). Справа от знака равно используется композиция в исходной категории \(\mathcal{A}\).
Тождественная стрелка – это естественное преобразование \(\eta\).
Можно показать, что категория Клейсли действительно является категорией и свойства операций композиции и тождества выполнены.
Интересно, что если в категории \(\mathcal{A}\) перевернуть все стрелки, то снова получится категория. Попробуйте нарисовать граф со стрелками, и затем мысленно переверните направление всех стрелок. Все пути исходного графа перейдут в перевёрнутые пути нового графа. При этом пути будут проходить через те же точки. Сохранятся композиции стрелок, только все они будут перевёрнуты. Такую категорию обозначают \(\mathcal{A}^{op}\). Но оказывается, что переворачивать мы можем не только категории но и свойства категорий, или утверждения о категориях, эту операцию называют дуализацией. Определим её:
| \(dual\ A\) | \(\quad = \quad\) | \(A\) | \(\qquad\) | если \(A\) является объектом |
| \(dual\ x\) | \(\quad = \quad\) | \(x\) | если \(x\) обозначает стрелку | |
| \(dual\ (f : A \rightarrow B)\) | \(\quad = \quad\) | \(dual\ f : B \rightarrow A\) | \(A\) и \(B\) поменялись местами | |
| \(dual\ (f \:\mathbf{;}\:g)\) | \(\quad = \quad\) | \(dual\ g \:\mathbf{;}\:dual\ f\) | \(f\) и \(g\) поменялись местами | |
| \(dual\ (id_A)\) | \(\quad = \quad\) | \(id_A\) |
Есть такое свойство: если в исходной категории \(\mathcal{A}\) выполняется какое-то утверждение, то в перевёрнутой категории \(\mathcal{A}^{op}\) выполняется перевёрнутое (дуальное) свойство. Часто в теории категорий из одних понятий получают другие дуализацией. При этом мы можем не проверять свойства для нового понятия - они будут выполняться автоматически. К дуальным понятиям обычно добавляют приставку “ко”. Приведём пример, получим понятие комонады.
Для начала вспомним определение монады. Монада – это эндофунктор (функтор, у которого совпадают начало и конец или домен и кодомен) \(T : \mathcal{A}\rightarrow \mathcal{A}\) и два естественных преобразования \(\eta : I \rightarrow T\) и \(\mu : TT \rightarrow T\), такие что выполняются свойства:
\(T \eta \:\mathbf{;}\:\mu = id\)
\(T \mu \:\mathbf{;}\:\mu = \mu \:\mathbf{;}\:\mu\)
Дуализируем это определение. Комонада – это эндофунктор \(T : \mathcal{A}\rightarrow \mathcal{A}\) и два естественных преобразования \(\eta : T \rightarrow I\) и \(\mu : T \rightarrow TT\), такие, что выполняются свойства
\(\mu \:\mathbf{;}\:T \eta = id\)
\(\mu \:\mathbf{;}\:T \mu = \mu \:\mathbf{;}\:\mu\)
Мы просто переворачиваем домены и кодомены в стрелках и меняем порядок в композиции. Проверьте, сошлись ли типы. Попробуйте нарисовать графическую схему свойств комонады и сравните со схемой для монады.
Можно также определить и категорию коКлейсли. В категории коКлейсли все стрелки имеют вид \(TA \rightarrow B\). Теперь дуализируем композицию из категории Клейсли:
\[f \:\mathbf{;_{T}}\:g = f \:\mathbf{;}\:Tg \:\mathbf{;}\:\mu\]
Теперь получим композицию в категории коКлейсли:
\[g \:\mathbf{;_{T}}\:f = \mu \:\mathbf{;}\:Tg \:\mathbf{;}\:f\]
Мы перевернули цепочки композиций слева и справа от знака равно. Проверьте, сошлись ли типы. Не забывайте, что в этом определении \(\eta\) и \(\mu\) естественные преобразования для комонады. Нам не нужно проверять, является ли категория коКлейсли действительно категорией. Нам не нужно опять проверять свойства стрелки тождества и ассоциативности композиции, если мы уже проверили их для монады. Следовательно, перевёрнутое утверждение будет выполняться в перевёрнутой категории коКлейсли. В этом основное преимущество определения через дуализацию.
Этим приёмом мы можем воспользоваться и в Haskell, дуализируем класс Monad:
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
Перевернём все стрелки:
class Comonad c where
coreturn :: c a -> a
cobind :: c b -> (c b -> a) -> c a
Представим, что в нашей категории есть такой объект \(0\), который соединён со всеми объектами, причём стрелка начинается из этого объекта, и для каждого объекта может быть только одна стрелка, которая соединят данный объект с \(0\). Графически эту ситуацию можно изобразить так:
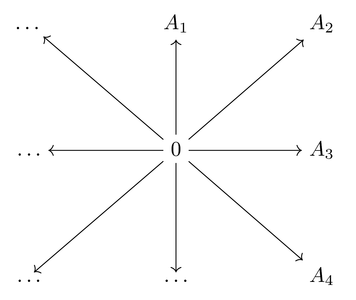
Такой объект называют начальным (initial object). Его принято обозначать нулём, словно это начало отсчёта. Для любого объекта \(A\) из категории \(\mathcal{A}\) с начальным объектом \(0\) существует и только одна стрелка . Можно сказать, что начальный объект определяет функцию, которая переводит объекты \(A\) в стрелки \(f : 0 \rightarrow A\). Эту функцию обозначают специальными скобками \((\hspace{-1.8pt}|\,\cdot\,|\hspace{-1.8pt})\), она называется катаморфизмом (catamorphism).
\[(\hspace{-1.8pt}|\,A\,|\hspace{-1.8pt}) = f : 0 \rightarrow A\]
У начального объекта есть несколько важных свойств. Они очень часто встречаются в разных вариациях, в понятиях, которые определяются через понятие начального объекта:
| \((\hspace{-1.8pt}|\,0\,|\hspace{-1.8pt}) = id_0\) | \(\qquad\) | \(\text{тождество}\) | ||
| \(f, g : 0 \rightarrow A\) | \(\Rightarrow \) | \(f = g\) | \(\text{уникальность}\) | |
| \(f: A \rightarrow B\) | \(\Rightarrow \) | \((\hspace{-1.8pt}|\,A\,|\hspace{-1.8pt}) \:\mathbf{;}\:f = (\hspace{-1.8pt}|\,B\,|\hspace{-1.8pt})\) | \(\text{слияние (fusion)}\) |
Эти свойства следуют из определения начального объекта. Свойство тождества говорит о том, что стрелка, ведущая из начального объекта в начальный, является тождественной стрелкой. В самом деле, по определению начального объекта для каждого объекта может быть только одна стрелка, которая начинается в \(0\) и заканчивается в этом объекте. Стрелка \((\hspace{-1.8pt}|\,0\,|\hspace{-1.8pt})\) начинается в \(0\) и заканчивается в \(0\), но у нас уже есть одна такая стрелка - по определению категории для каждого объекта определена тождественная стрелка - значит эта стрелка является единственной.
Второе свойство следует из единственности стрелки, ведущей из начального объекта в данный. Третье свойство лучше изобразить графически:

Поскольку стрелки \((\hspace{-1.8pt}|\,A\,|\hspace{-1.8pt})\) и \(f\) можно соединить, то должна быть определена стрелка \((\hspace{-1.8pt}|\,A\,|\hspace{-1.8pt}) \:\mathbf{;}\:f : 0 \rightarrow B\), но поскольку в категории с начальным объектом из начального объекта \(0\) в объект \(B\) может вести лишь одна стрелка, то стрелка \((\hspace{-1.8pt}|\,A\,|\hspace{-1.8pt}) \:\mathbf{;}\:f\) должна совпадать с \((\hspace{-1.8pt}|\,B\,|\hspace{-1.8pt})\).
Дуализируем понятие начального объекта. Пусть в категории \(\mathcal{A}\) есть объект \(1\), такой что для любого объекта \(A\) существует и только одна стрелка, которая начинается из этого объекта и заканчивается в объекте \(1\). Такой объект называют конечным (terminal object):

Конечный объект определяет в категории функцию, которая ставит в соответствие объектам стрелки, которые начинаются из данного объекта и заканчиваются в конечном объекте. Такую функцию называют анаморфизмом (anamorphism), и обозначают специальными скобками \([\hspace{-2.4pt}(\,\cdot\,)\hspace{-2.4pt}]\), которые похожи на перевёрнутые скобки для катаморфизма:
\[[\hspace{-2.4pt}(\,A\,)\hspace{-2.4pt}] = f : A \rightarrow 1\]
Можно дуализировать и свойства:
| \([\hspace{-2.4pt}(\,1\,)\hspace{-2.4pt}] = id_1\) | \(\qquad\) | тождество | ||
| \(f, g : A \rightarrow 1\) | \(\Rightarrow \) | \(f = g\) | уникальность | |
| \(f: A \rightarrow B\) | \(\Rightarrow \) | \(f \:\mathbf{;}\:[\hspace{-2.4pt}(\,B\,)\hspace{-2.4pt}] = [\hspace{-2.4pt}(\,A\,)\hspace{-2.4pt}]\) | слияние (fusion) |
Приведём иллюстрацию для свойства слияния:

Давным-давно, когда мы ещё говорили о типах, мы говорили, что типы конструируются с помощью двух базовых операций: суммы и произведения. Сумма говорит о том, что значение может быть либо одним значением, либо другим. А произведение обозначает сразу несколько значений. В Haskell есть два типа, которые представляют собой сумму и произведение в общем случае. Тип для суммы это Either:
data Either a b = Left a | Right b
Произведение в самом общем виде представлено кортежами:
data (a, b) = (a, b)
В теории категорий сумма и произведение определяются как начальный и конечный объекты в специальных категориях. Теория категорий изучает объекты по тому, как они взаимодействуют с остальными объектами. Взаимодействие обозначается с помощью стрелок. Специальные свойства стрелок определяют объект.
Например, представим, что мы не можем заглядывать внутрь суммы типов. Как бы мы могли взаимодействовать с объектом, который представляет собой сумму двух типов \(A+B\)? Нам необходимо уметь создавать объект типа \(A+B\) из объектов \(A\) и \(B\) и извлекать их из суммы. Создание объектов происходит с помощью двух специальных конструкторов:
\[inl : A \rightarrow A+B\]
\[inr : B \rightarrow A+B\]
Также нам хочется как-то извлекать значения. По смыслу внутри суммы \(A+B\) хранится либо объект \(A\),
либо объект \(B\), и мы не можем заранее знать какой из них, поскольку внутреннее содержание \(A+B\) от нас скрыто, но мы знаем, что это только \(A\) или \(B\). Это говорит о том, что если у нас есть две стрелки \(A \rightarrow C\) и \(B \rightarrow C\), то мы как-то можем построить \(A+B \rightarrow C\). У нас есть операция:
\[out(f,g) : A+B \rightarrow C \qquad f : A \rightarrow C,\ g : B \rightarrow C\]
При этом для того, чтобы стрелки \(inl\), \(inr\) и \(out\) были согласованы необходимо, чтобы выполнялись свойства:
\[inl \:\mathbf{;}\:out(f,g)\ =\ f\]
\[inr \:\mathbf{;}\:out(f,g)\ =\ g\]
для любых функций \(f\) и \(g\). Графически это свойство можно изобразить так:
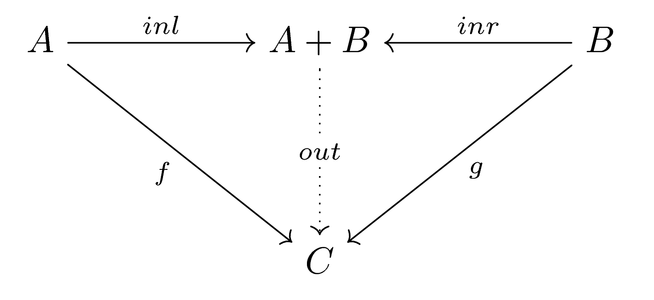
Итак, суммой двух объектов \(A\) и \(B\) называется объект \(A+B\) и две стрелки \(inl : A \rightarrow A+B\) и \(inr : B \rightarrow A+B\) такие, что для любых двух стрелок \(f : A \rightarrow C\) и \(g : B \rightarrow C\) определена одна и только одна стрелка \(h : A+B \rightarrow C\) такая, что выполнены свойства:
\[inl \:\mathbf{;}\:h = f\] \[inr \:\mathbf{;}\:h = g\]
В этом определении объект \(A+B\) вместе со стрелками \(inl\) и \(inr\), определяет функцию, которая по некоторому объекту \(C\) и двум стрелкам \(f\) и \(g\) строит стрелку \(h\), которая ведёт из объекта \(A+B\) в объект \(C\). Этот процесс определения стрелки по объекту напоминает определение начального элемента. Построим специальную категорию, в которой объект \(A+B\) будет начальным. Тогда функция \(out\) будет катаморфизмом.
Функция \(out\) принимает две стрелки и возвращает третью. Посмотрим на типы:
\[f : A \rightarrow C \qquad\qquad inl : A \rightarrow A+B\]
\[g : B \rightarrow C \qquad\qquad inr : B \rightarrow A+B\]
Каждая из пар стрелок в столбцах указывают на один и тот же объект, а начинаются они из двух разных объектов \(A\) и \(B\). Определим категорию, в которой объектами являются пары стрелок \((a_1, a_2)\), которые начинаются из объектов \(A\) и \(B\) и заканчиваются в некотором общем объекте \(D\). Эту категорию ещё называют клином. Стрелками в этой категории будут такие стрелки \(f : (d_1, d_2) \rightarrow (e_1, e_2)\), что стрелки в следующей диаграмме коммутируют (не важно по какому пути идти из двух разных точек).

Композиция стрелок – это обычная композиция в исходной категории, в которой определены объекты \(A\) и \(B\), а тождественная стрелка для каждого объекта – это тождественная стрелка для того объекта, в котором сходятся обе стрелки. Можно проверить, что это действительно категория.
Если в этой категории есть начальный объект, то мы будем называть его суммой объектов \(A\) и \(B\). Две стрелки, которые содержит этот объект мы будем называть \(inl\) и \(inr\), а общий объект, в котором эти стрелки сходятся, будем называть \(A+B\). Теперь если мы выпишем определение для начального объекта, но вместо произвольных стрелок и объектов подставим наш конкретный случай, то мы получим как раз исходное определение суммы.
Начальный объект \((inl : A \rightarrow A+B,\ inr : B \rightarrow A+B)\) ставит в соответствие любому объекту \((f : A \rightarrow C,\ g : B \rightarrow C)\) стрелку \(h : A+B \rightarrow C\) такую, что выполняются свойства:
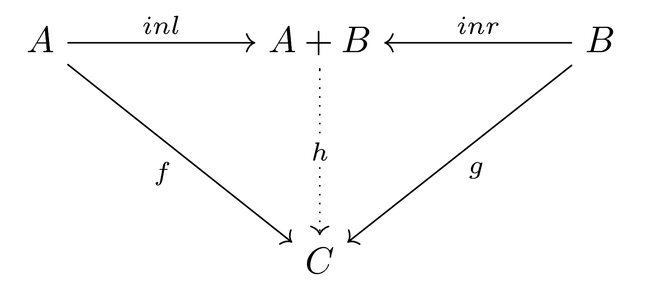
А как на счёт произведения? Оказывается, что произведение является дуальным понятием по отношению к сумме. Его иногда называют косуммой, или сумму называют копроизведением. Дуализируем категорию, которую мы строили для суммы.
У нас есть категория \(\mathcal{A}\) и в ней выделено два объекта \(A\) и \(B\). Объектами новой категории будут пары стрелок \((a_1,a_2)\), которые начинаются в общем объекте \(C\), а заканчиваются в объектах \(A\) и \(B\). Стрелками в этой категории будут стрелки исходной категории \(h : (e_1,e_2) \rightarrow (d_1,d_2)\) такие, что следующая диаграмма коммутирует:

Композиция и тождественные стрелки позаимствованы из исходной категории \(\mathcal{A}\). Если в этой категории существует конечный объект, то мы будем называть его произведением объектов \(A\) и \(B\). Две стрелки этого объекта обозначаются как \((exl,exr)\), а общий объект из которого они начинаются мы назовём \(A\times B\). Теперь распишем определение конечного объекта для нашей категории пар стрелок с общим началом.
Конечный объект \((exl : A \times B \rightarrow A, \ exr : A \times B \rightarrow B)\) ставит в соответствие любому объекту категории \((f : C \rightarrow A,\ g : C \rightarrow B)\) стрелку \(h : C \rightarrow A \times B\). При этом выполняются свойства:

Итак, мы определили сумму, а затем на автомате, перевернув все утверждения, получили определение произведения. Но что это такое? Соответствует ли оно интуитивному понятию произведения?
Так же как и в случае суммы в теории категорий мы определяем понятие через то, как мы можем с ним взаимодействовать. Посмотрим, что нам досталось от абстрактного определения. У нас есть обозначение произведения типов \(A \times B\). Две стрелки \(exl\) и \(exr\). Также у нас есть способ получить по двум функциям \(f : C \rightarrow A\) и \(g : C \rightarrow B\) стрелку \(h : C \rightarrow A \times B\). Для начала посмотрим на типы стрелок конечного объекта:
\[exl : A \times B \rightarrow A\]
\[exr : A \times B \rightarrow B\]
По типам видно, что эти стрелки разбивают пару на составляющие. По смыслу произведения мы точно знаем, что у нас есть в \(A\times B\) и объект \(A\) и объект \(B\). Эти стрелки позволяют нам извлекать компоненты пары. Теперь посмотрим на анаморфизм:
\[[\hspace{-2.4pt}(\,f,g\,)\hspace{-2.4pt}] : C \rightarrow A \times B \qquad f : C \rightarrow A,\ g : C \rightarrow B\]
Эта функция позволяет строить пару по двум функциям и начальному значению. Но, поскольку здесь мы ничего не вычисляем, а лишь связываем объекты, мы можем по паре стрелок, которые начинаются из общего источника связать источник с парой конечных точек \(A \times B\).
При этом выполняются свойства:
\[[\hspace{-2.4pt}(\,f,g\,)\hspace{-2.4pt}] \:\mathbf{;}\:exl = f\]
\[[\hspace{-2.4pt}(\,f,g\,)\hspace{-2.4pt}] \:\mathbf{;}\:exr = g\]
Эти свойства говорят о том, что функции построения пары и извлечения элементов из пары согласованы. Если мы положим значение в первый элемент пары и тут же извлечём его, то это тоже само если бы мы не использовали пару совсем. То же самое и со вторым элементом.
Если представить, что стрелки это функции, то может показаться, что все наши функции являются функциями одного аргумента. Ведь у стрелки есть только один источник. Как быть если мы хотим определить функцию нескольких аргументов, что она связывает? Если в нашей категории определено произведение объектов, то мы можем представить функцию двух аргументов, как стрелку, которая начинается из произведения:
\[(+) : Num \times Num \rightarrow Num\]
Но в лямбда-исчислении нам были доступны более гибкие функции, функции могли принимать на вход функции и возвращать функции. Как с этим обстоят дела в теории категорий? Если перевести определение функций высшего порядка на язык теории категорий, то мы получим стрелки, которые могут связывать другие стрелки. Категория с функциями высшего порядка может содержать свои стрелки в качестве объектов. Стрелки как объекты обозначаются с помощью степени, так запись \(B^A\) означает стрелку \(A \rightarrow B\). При этом нам необходимо уметь интерпретировать стрелку, мы хотим уметь подставлять значения. Если у нас есть объект \(B^A\), то должна быть стрелка
\[eval : B^A \times A \rightarrow B\]
На языке функций можно сказать, что стрелка \(eval\) принимает функцию высшего порядка \(A \rightarrow B\) и значение типа \(A\), а возвращает значение типа \(B\). Объект \(B^A\) называют экспонентой. Теперь дадим формальное определение.
Пусть в категории \(\mathcal{A}\) определено произведение. Экспонента – это объект \(B^A\) вместе со стрелкой \(eval : B^A \times A \rightarrow B\) такой, что для любой стрелки \(f : C \times A \rightarrow B\) определена стрелка \(curry(f):C \rightarrow B^A\) при этом следующая диаграмма коммутирует:

Давайте разберёмся, что это всё означает. По смыслу стрелка \(curry(f)\) это каррированная функция двух аргументов. Вспомните о функции curry из Haskell. Диаграмма говорит о том, что если мы каррированием функции двух аргументов получим функцию высшего порядка \(C \rightarrow B^A\), а затем с помощью функции \(eval\) получим значение, то это всё равно, что подставить два значения в исходную функцию. Запись \((curry(f), id)\) означает параллельное применение двух стрелок внутри пары:
\[(f, g) : A \times A' \rightarrow B \times B' , \qquad f : A\rightarrow B , \ g : A' \rightarrow B'\]
Так применив стрелки \(curry(f) : C \rightarrow B^A\) и \(id : A \rightarrow A\) к паре \(C \times A\), мы получим пару \(B^A \times A\). Применение здесь условное мы подразумеваем применение в функциональной аналогии, в теории категорий происходит связывание пар объектов с помощью стрелки \((f, g)\).
Интересно, что и экспоненту можно получить как конечный объект в специальной категории. Пусть есть категория \(\mathcal{A}\) и в ней определено произведение объектов \(A\) и \(B\). Построим категорию, в которой объектами являются стрелки вида:
\[C \times A \rightarrow B\]
где \(C\) – это произвольный объект исходной категории. Стрелкой между объектами \(c : C \times A \rightarrow B\) и \(d : D \times A \rightarrow B\) в этой категории будет стрелка \(f : C \rightarrow D\) из исходной категории, такая, что следующая диаграмма коммутирует:
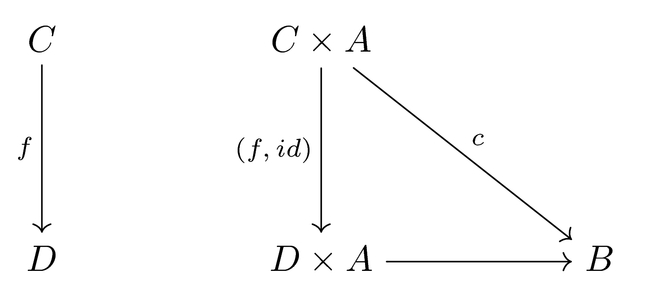
Если в этой категории существует конечный объект, то он является экспонентой. А функция \(curry\) является анаморфизмом для экспоненты.
Теория категорий изучает понятия через то, как эти понятия взаимодействуют друг с другом. Мы забываем о том, как эти понятия реализованы, а смотрим лишь на свойства связей.
Мы узнали, что такое категория. Категория это структура с объектами и стрелками. Стрелки связывают объекты. Причём связи могут соединятся. Также считается, что объект всегда связан сам с собой. Мы узнали, что есть такие категории, в которых сами объекты являются категориями, а стрелки в таких категориях мы назвали функторами. Также мы узнали, что сами функторы могут стать объектами в некоторой категории, тогда стрелки в этой категории мы назвали естественными преобразованиями.
Мы узнали, что такое начальный и конечный объект и как с помощью этих понятий можно определить сумму и произведение типов. Также мы узнали как в теории категорий описываются функции высших порядков.
Проверьте аксиомы категории (ассоциативность и тождество) для категории функторов и категории естественных преобразований.
Изоморфизмом называют такие стрелки \(f:A \rightarrow B\) и \(g : B \rightarrow A\), для которых выполнено свойство:
\[f \:\mathbf{;}\:g = id_A\] \[g \:\mathbf{;}\:f = id_B\]
Объекты \(A\) и \(B\) называют изоморфными, если они связаны изоморфизмом, это обозначают так: \(A \cong B\). Докажите, что все начальные и конечные элементы изоморфны.
Поскольку сумма и произведение типов являются начальным и конечным объектами в специальных категориях для них также выполняются свойства тождества, уникальности и слияния. Выпишите эти свойства для суммы и произведения.
Подумайте как можно определить экземпляр класса Comonad для потоков:
data Stream a = a :& Stream a
Можно ли придумать экземпляр для класса Monad?
Дуальную категорию для категории \(\mathcal{A}\) обозначают \(\mathcal{A}^{op}\). Если \(F\) является функтором в категории \(\mathcal{A}^{op}\), то в исходной категории его называют контравариантным функтором. Выпишите определение функтора в \(\mathcal{A}^{op}\), а затем с помощью дуализации получите свойства контравариантного функтора в исходной категории \(\mathcal{A}\).